BÀI TẬP CUỐI CHƯƠNG VIII

PHẦN I. HỆ THỐNG BÀI TẬP, BÀI GIẢI CUỐI SGK

1. HỆ THỐNG BÀI TẬP CUỐI SGK

Bài 1: Trong các khẳng định sau, khẳng định nào đúng?

A. Hai tam giác đồng dạng thì bằng nhau

B. Hai tam giác bằng nhau thì đồng dạng

C. Hai tam giác bằng nhau thì không đồng dạng

D. Hai tam giác cân thì luôn đồng dạng

Bài 2: Nếu ΔABC ᔕ ΔMNP theo tỉ số k = 3 thì ΔMNP ᔕ ΔABC theo tỉ số

A.                         B. 19                      C. 3                        D. 9

Bài 3: Nếu tam giác ABC có MN // AB (với M ∈ AC, N ∈ BC) thì

A. ΔCMN ᔕ ΔABC                                       B. ΔCNM ᔕ ΔCAB

C. ΔCNM ᔕ ΔABC                                       D. ΔMNC ᔕ ΔABC

Bài 4: Cho ΔABD ᔕ ΔDEF với tỉ số đồng dạng k = , biết AB = 9 cm. Khi đó DE bằng

A. 6 cm                  B. 12 cm                C. 3 cm                  D. 27 cm

Bài 5:  Nếu tam giác ABC và tam giác EFG có  ;  thì

A. ΔABC ᔕ ΔEGF                                        B. ΔABC ᔕ ΔEFG

C. ΔACB ᔕ ΔGFE                                         D. ΔCBA ᔕ ΔFGE

Bài 6: Cho ΔXYZ ᔕ ΔEFG, biết XY = 6 cm; EF = 8 cm; EG = 12 cm. Khi đó XZ bằng

A. 10 cm                B. 9 cm                  C. 12 cm                D. 16 cm

Bài 7: Cho ΔABC ᔕ ΔDEF, biết = 85⁰ ; = 60⁰.Khi đó số đo bằng

A. 60°                               B. 85°                     C. 35°                    D. 45°

Bài 8: Cho hình thang ABCD (AB//CD), có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 8 cm, CD = 20 cm. Khi đó ΔAOB ᔕ ΔCOD với tỉ số đồng dạng là

A. k =                  B. k =                   C. k =                  D. k =

Bài 9: Trong Hình 1, cho biết  , AC = 9 cm, AD = 4 cm

a) Chứng minh tam giác ΔABD ᔕ ΔACB

b) Tính độ dài cạnh AB

Bài 10: a) Cho hình thang ABCD (AB // CD), biết = (Hình 2a). Chứng minh rằng BD² =AB.CD

b) Cho hình thang EFGH (EF // GH), = , EF = 9 m, GH = 16 m (Hình 2b). Tính độ dài x của HF

Bài 11: a) Tính khoảng cách HM của mặt hồ ở Hình 3a

b) Tính khoảng cách MN của một khúc sông ở hình 3b

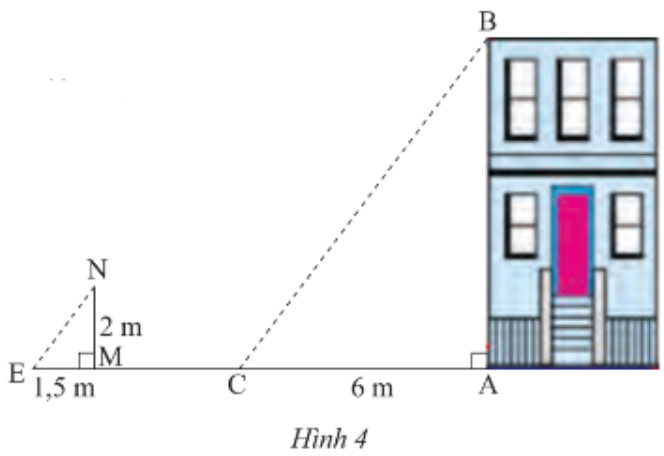
Bài 12: Bóng của một căn nhà trên mặt đất có độ dài 6m. Cùng thời điểm đó, một cọc sắt cao 2m cắm vuông góc với mặt đất có bóng dài 1,5 m (Hình 4). Tính chiều cao ngôi nhà

Bài 13: Người ta đo khoảng cách giữa hai điểm D và K ở hai bờ một dòng sông (Hình 5). Cho biết KE = 90 m, KF = 160 m. Tính khoảng cách DK

Bài 14: Cho tam giác ABC nhọn có hai đường cao BE, CF cắt nhau tại H. Chứng minh rằng

a) ΔAEB ᔕ ΔAFC

b)

c) ΔHEF ᔕ ΔHCB

Bài 15: Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H

a) Chứng minh rằng ΔAMN ᔕ ΔABC

b) Phân giác của cắt MN và BC lần lượt tại I và K. 

    Chứng minh rằng

Bài 16: Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC).

a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB² =BH.BC

b) Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F. Chứng minh rằng AE. AB = AF.AC

c) Chứng minh rằng ΔAFE ᔕ ΔABC

d) Qua A vẽ đường thẳng song song với BC cắt đường thẳng HF tại I. Vẽ IN vuông góc BC tại N. Chứng minh rằng ΔHNF ᔕ ΔHIC

Bài 17: Quan sát Hình 6.Vẽ vào tờ giấy tam giác DEF với EF = 4cm, =36⁰, =76⁰

a) Chứng minh ΔDEF ᔕ ΔAMC

b) Dùng thước đo chiều dài cạnh DF của ΔDEF. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 6

2. 5 PHÚT GIẢI BÀI CUỐI SGK

Đáp án bài 9: 

a) chung; = => ΔABD ᔕ ΔACB (g.g)

b) AB = 6cm

Đáp án bài 10: 

a) ΔABD ᔕ ΔBDC (g.g) => hay BD² = AB.CD

b) HF = 12 (cm) 

Đáp án bài 11: a) HM = 20 (m); b) MN = (m)

Đáp án bài 12: 8 m

Đáp án bài 13: DK = 120 (m)

Đáp án bài 14: 

a) Xét tam giác vuông AEB và AFC: chung => ΔAEB ᔕ ΔAFC (g.g)

b) ΔHCE ᔕ ΔHBF (g.g) => hay

c) ; = => ΔHEF ᔕ ΔHCB (c.g.c)

Đáp án bài 15: 

a) ; chung => ΔAMN ᔕ ΔABC (c.g.c)

b) ;  => = hay

Đáp án bài 16: 

a) Xét tam giác vuông ABH và CBA: chung  => ΔABH ᔕ ΔCBA 

AB² = BH. BC

b, c) Xét tam giác AEF và ACB: chung ; = ΔAEF ᔕ ΔACB (g.g) 

hay AE.AB = AF.AC

d) Xét tam giác HNF và HIC: chung ; ΔHNF ᔕ ΔHIC (c.g.c)

Đáp án bài 17: 

a) Xét tam giác DEF và AMC: = 36⁰ ; = = 76⁰ => ΔDEF ᔕ ΔAMC (g.g)

b) AC = (m)