A. TÓM TẮT LÝ THUYẾT

1. Đoạn thẳng tỉ lệ

Định nghĩa

AB, CD tỉ lệ với A'B', C'D' $\Leftrightarrow \frac{AB}{CD}=\frac{A'B'}{C'D'}$.

Tính chất

$\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}} \Leftrightarrow \left\{ \begin{array}{l}AB.C'D' = A'B'.CD\\\frac{{AB \pm CD}}{{CD}} = \frac{{A'B' \pm C'D'}}{{C'D'}}\\\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}} = \frac{{AB \pm A'B'}}{{CD \pm C'D'}}\end{array} \right.$

2. Định lí Ta-lét thuận và đảo

Cho tam giác ABC (h.61)

${\rm{a//BC}} \Rightarrow \left[ \begin{array}{l}\frac{{{\rm{AB'}}}}{{{\rm{AB}}}}{\rm{ = }}\frac{{{\rm{AC'}}}}{{{\rm{AC}}}}\\\frac{{{\rm{AB'}}}}{{{\rm{BB'}}}}{\rm{ = }}\frac{{{\rm{AC'}}}}{{{\rm{CC'}}}}\\\frac{{{\rm{BB'}}}}{{{\rm{AB}}}}{\rm{ = }}\frac{{{\rm{CC'}}}}{{{\rm{AC}}}}\end{array} \right.$

3. Hệ quả của định lí Ta-lét

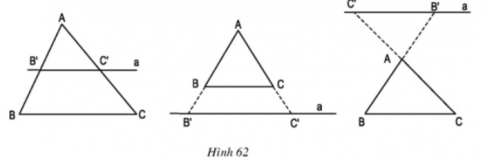
Cho tam giác ABC

$a//BC \Rightarrow \frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}$

4. Tính chất của đường phân giác trong tam giác

AD là tia phân giác của góc BAC, AE là tia phân giác của góc BAx (h. 63)

Ta có: $\frac{AB}{AC}=\frac{DB}{DC}=\frac{EB}{EC}$

5. Tam giác đồng dạng

Định nghĩa

$\Delta A'B'C' \sim \Delta ABC$ (tỉ số đồng dạng k)

$\Leftrightarrow \left\{ \begin{array}{l}\widehat {{\rm{A'}}}{\rm{ = }}\widehat {\rm{A}}{\rm{;}}\widehat {{\rm{B'}}}{\rm{ = }}\widehat {\rm{B}}{\rm{;}}\widehat {{\rm{C'}}}{\rm{ = }}\widehat {\rm{C}}\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A'}}{{CA}} = k\end{array} \right.$

Tính chất

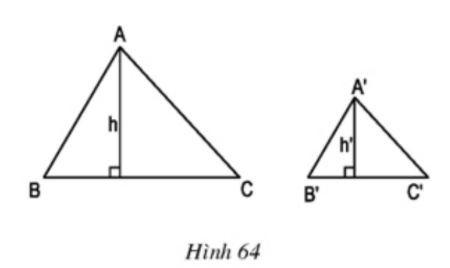
$\frac{h}{h'}=k$ (h'; h tương ứng là đường cao của tam giác A'B'C' và tam giác ABC)

$\frac{p'}{p}=k;\,\ \frac{S'}{S}=k^2$ (p'; p tương ứng là chu vi của tam giác A'B'C' và tam giác ABC; S', S tương ứng là diện tích của tam giác A'B'C' và tam giác ABC)

6. Các trường hợp đồng dạng của hai tam giác ABC và tam giác A'B'C'

Trường hợp 1: Cạnh - cạnh - cạnh

$\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A'}}{{CA}} \Rightarrow \Delta A'B'C' \sim \Delta ABC$

Trường hợp 2: Cạnh - góc - cạnh

$\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}};\,\ \widehat{B'}=\widehat{B} \Rightarrow \Delta A'B'C' \sim \Delta ABC$

Trường hợp 3: Góc - góc

$\widehat{A'}=\widehat{A};\,\ \widehat{B'}=\widehat{B} \Rightarrow \Delta A'B'C' \sim \Delta ABC$

7. Các trường hợp đồng dạng của tam giác vuông ABC và A'B'C' ($\widehat{A'}=\widehat{A}=90^0$)

Trường hợp 1:

$\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\Rightarrow \Delta A'B'C' \sim \Delta ABC$

Trường hợp 2:

         $\widehat{B'}=\widehat{B}\Rightarrow \Delta A'B'C' \sim \Delta ABC$

hoặc $\widehat{C'}=\widehat{C}\Rightarrow \Delta A'B'C' \sim \Delta ABC$

Trường hợp 3:

$\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}\Rightarrow \Delta A'B'C' \sim \Delta ABC$