NỘI DUNG TRẮC NGHIỆM

Câu 1: Cho ∆ABC có AH vừa là đường cao, vừa là đường phân giác. Hỏi ∆ABC chắc chắn là tam giác gì?

• A. Tam giác cân;

• B. Tam giác đều;
• C. Tam giác vuông;
• D. Tam giác nhọn.

Câu 2: Cho hình vẽ bên dưới:

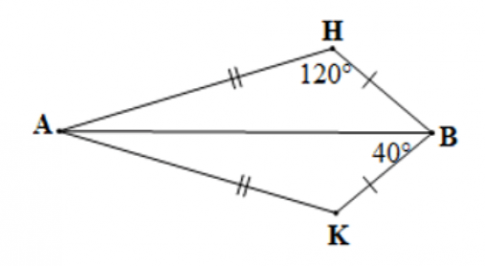
Số đo của $\widehat{KAB}$ trong hình vẽ trên bằng:

• A. 50°;
• B. 40°;
• C. 30°;

• D. 20°.

Câu 3: Biết 5(2x − 1) − 4(8 − 3x) = 84. Giá trị của x là:

• A. x = 4;
• B. x = 4,5;
• C. x = 5;

• D. x = 5,5.

Câu 4: Biểu đồ dưới đây cho biết số lượng máy tính bán được trong 6 tháng đầu năm của một cửa hàng.

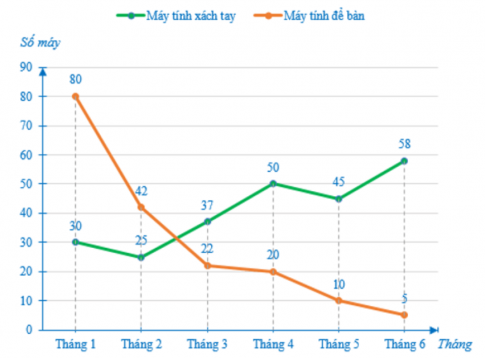
Khẳng định nào sau đây là đúng?

• A. Trong hai tháng đầu số lượng máy tính để bàn bán được ít hơn máy tính xách tay;
• B. Bốn tháng sau số lượng máy tính để bàn bán được ngày càng tăng;
• C. Tổng số lượng máy tính xách tay bán được trong 6 tháng là 179 máy;

• D. Tổng số lượng máy tính để bàn bán được trong 6 tháng là 179 máy.

Câu 5: Cho hình chữ nhật có chiều dài lớn hơn chiều rộng là 5 đơn vị. Biểu thức tính diện tích hình chữ nhật là:

• A. S = $x^2$ + 5x;

• B. S = 2($x^2$ + 5x);
• C. S = 2x + 5;
• D. S = $x^2$ – 5x.

Câu 6: Gieo một con xúc xắc 6 mặt cân đối. Tính xác suất của biến cố “Gieo được mặt có số chấm nhiều hơn 6”.

• A. 0;

• B. 0,2;
• C. 0,4;
• D. 1.

Câu 7: Cho biểu thức P(x) = $x^2$($x^2$ + x + 1) – 3x(x – a) + 4. Tìm a sao cho tổng các hệ số của đa thức bằng –2.

• A. –1;
• B. 1;

• C. –2;

• D. 2.

Câu 8: Cho hình vẽ bên dưới:

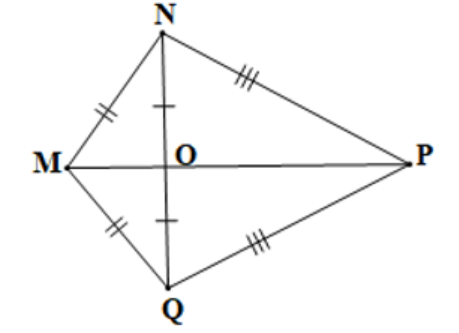
Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:

• A. 1;
• B. 2;

• C. 3;

• D. 4.

Câu 9: Cho biểu đồ biểu diễn số bánh mì bán được tại căng tin trường vào các ngày trong tuần vừa qua:

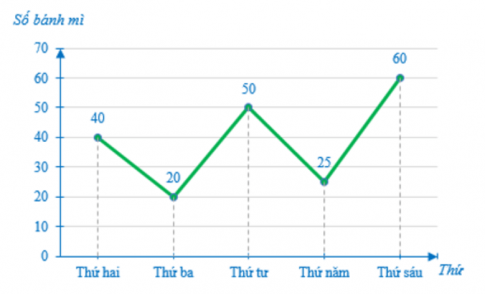
Bảng thống kê số liệu nào phù hợp với biểu đồ trên?

A. 

B. 

C.

D.

Câu 10: Giả sử 3 kích thước của một hình hộp chữ nhật là x; x + 1; x – 1 (cm) với x > 1. Thể tích hình hộp chữ nhật này là:

• A. $x^3$ + x ($cm^3$)

• B. $x^3$ – x ($cm^3$)

• C. $x^2$ + x ($cm^3$)
• D. $x^2$ – x ($cm^3$)

Câu 11: Cho tam giác IOH, vẽ cung tròn tâm I bán kính OH, vẽ cung tròn tâm O bán kính IH, hai cung tròn này cắt nhau tại K (K và H nằm khác phía so với đường thẳng IO). Khẳng định nào sau đây là đúng nhất?

• A. HO // KI;
• B. OK // IH;
• C. Cả A và B đều sai;

• D. Cả A và B đều đúng.

Câu 12: Cho ∆ABC cân tại A. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của ∆ABC. Kẻ AH ⊥ BC tại H. Khẳng định nào sau đây sai?

• A. AI ⊥ BC;
• B. HB = HC;

• C. AI // IH;

• D. AH trùng AI.

Câu 13: Cho biểu đồ biểu diễn tỉ lệ số dân của các châu lục tính đến ngày 01/07/2020.

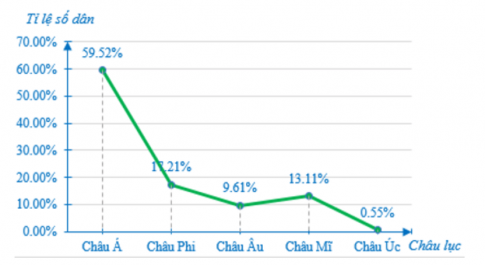
Biết rằng năm 2020 tổng số dân của 5 châu lục là 7 773 triệu người. Theo em, số dân của châu Á hơn số dân của châu Âu bao nhiêu người?

• A. 3879,5043 triệu người;

• B. 3879,5034 triệu người;
• C. 3897,5043 triệu người;
• D. 3897,5034 triệu người.

Câu 14: Gieo ngẫu nhiên xúc xắc một lần. Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia hết cho 2”. Xác suất của biến cố này là:

• A. $\frac{1}{2}$

• B. $\frac{1}{4}$
• C. $\frac{1}{3}$
• D. $\frac{1}{5}$

Câu 15: Cho hai hình chữ nhật như hình vẽ.

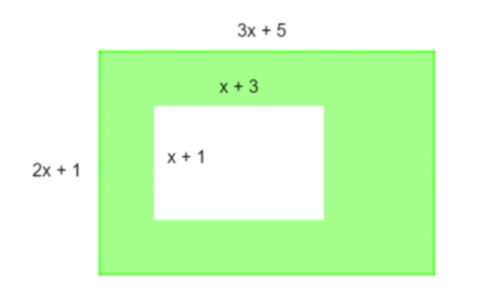
Đa thức theo biến x biểu thị diện tích của phần được tô màu xanh là:

• A. 5x2 + 17x + 8 

• B. 5x2 + 9x + 2 

• C. 5x2 + 17x – 2 
• D. 5x2 – 9x – 2 

Câu 16: Cho A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11)

Và B = x(2x + 1) – $x^2$(x + 2) + $x^3$ – x + 3.

Chọn khẳng định đúng trong các khẳng định sau:

• A. A = B;
• B. A = 25B;

• C. A = 25B + 1;

• D. A = 2B.

Câu 16: Tính tổng các hệ số của lũy thừa bậc ba, lũy thừa bậc hai và lũy thừa bậc nhất trong kết quả của phép nhân (x2 + x + 1)(x3 – 2x + 1) ta được kết quả:

• A. 1;
• B. –2;

• C. –3;

• D. 3.

Câu 17: Cho hai tam giác MNP và OHK có MN = OH, NP = HK. Điều kiện để ∆NMP = ∆HOK theo trường hợp cạnh – cạnh – cạnh là:

• A. MP = OH;
• B. MN = KH;

• C. MP = OK;

• D. Không có điều kiện nào thoả mãn.

Câu 18: Tung hai đồng xu cân đối một số lần ta được kết quả như sau:

Xác suất của biến cố “Một đồng sấp, một đồng ngửa” là:

• A. $\frac{1}{5}$

• B. $\frac{2}{5}$

• C. $\frac{3}{5}$
• D. $\frac{4}{5}$

Câu 19: Cho ∆ABC có CF là tia phân giác của $\widehat{C}$ (F ∈ AB). Qua F kẻ đường thẳng song song với BC cắt AC ở E. Trên cạnh BC lấy điểm D sao cho CD = FE. FC là đường phân giác của tam giác nào?

• A. ∆DEF;

• B. ∆BEF;
• C. Cả A và B đều đúng.
• D. Cả A và B đều sai.

Câu 20: Cho tam giác NMP (NP < MN). Trên cạnh MN lấy điểm E sao cho NE = NP. Lấy Q là trung điểm của PE. Qua M kẻ đường thẳng vuông góc với PE tại F. Chọn khẳng định đúng:

• A. $\widehat{C}$ = $80^{\circ}$

• B. FM // NQ;

• C. ∆ENQ = ∆PQN;
• D. Cả A, B, C đều đúng.

Câu 21: Cho tam giác DEG (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh I, H, K. Biết $\widehat{D}$ = $\widehat{K}$, $\widehat{G}$ =$\widehat{I}$. Kí hiệu về sự bằng nhau của hai tam giác là:

• A. ∆DEG = ∆IHK;
• B. ∆DEG = ∆HIK;
• C. ∆DEG = ∆KIH;

• D. ∆DEG = ∆KHI.

Câu 22: Tính tổng các hệ số của lũy thừa bậc ba, lũy thừa bậc hai và lũy thừa bậc nhất trong kết quả của phép nhân ($x^2$ + x + 1)($x^3$ – 2x + 1) ta được kết quả:

• A. 1;
• B. –2;

• C. –3;

• D. 3.

Câu 23: Tính (12$x^4$) : (3$x^2$)

• A. 4x;
• B. 4$x^2$;
• C. –4x;
• D. –4$x^2$.

Câu 24: Cho ∆ABC cân tại A. Gọi M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại E. Điểm E thuộc đường thẳng nào trong các đường thẳng sau đây.

• A. BC;

• B. AM;

• C. AB;
• D. AC.

Câu 25: Cho ∆ABC nhọn có H là trực tâm. Trực tâm của ∆HAB là:

• A. Điểm B;
• B. Điểm H;

• C. Điểm C;

• D. Điểm A.

Câu 26: Trong trò chơi gieo xúc xắc, số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là 6. Nếu k là số các kết quả thuận lợi cho biến cố thì xác xuất của biến cố là:

• A. $\frac{k}{6}$

• B. $\frac{2k}{6}$
• C. $\frac{3k}{6}$
• D. $\frac{4k}{6}$

Câu 27: Chọn câu đúng.

• A. (x – 1)($x^2$ + x + 1) = $x^3$ – 1;

• B. (x – 1)(x + 1) = 1 – $x^2$;
• C. (x + 1)(x – 1) = $x^2$ + 1;
• D. ($x^2$ + x + 1)(x – 1) = 1 – $x^2$.

Câu 28: Cho ∆ABC cân tại A có M là trung điểm BC, đường cao CN cắt AM tại H. Một tính chất của cặp đường thẳng BH và AC là:

• A. BH // AC;
• B. BH trùng AC;
• C. BH cắt AC nhưng không vuông góc với AC;

• D. BH ⊥ AC.

Câu 29: Cho ∆ABC có AH vừa là đường cao, vừa là đường phân giác. Hỏi ∆ABC chắc chắn là tam giác gì?

• A. Tam giác cân;

• B. Tam giác đều;
• C. Tam giác vuông;
• D. Tam giác nhọn.

Câu 30: Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng.

• A. B ⁝ 10 với mọi m $\in  \mathbb{Z}$

• B. B ⁝ 15 với mọi m $\in  \mathbb{Z}$
• C. B ⁝ 9 với mọi m $\in  \mathbb{Z}$
• D. B ⁝ 20 với mọi m $\in  \mathbb{Z}$

Câu 31: Cho ∆ABC cân tại A. Gọi H là trực tâm của ∆ABC và $\widehat{BAH} = 30^{\circ}$. Xét hai khẳng định sau:

(I) ∆ABC là tam giác vuông cân;

(II) ∆ABC là tam giác đều.

Chọn câu trả lời đúng.

• A. Chỉ (I) đúng;

• B. Chỉ (II) đúng;

• C. Cả (I) và (II) đều đúng;
• D. Cả (I) và (II) đều sai.

Câu 32: Cho ∆ABC có M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại O. Số đo $\widehat{OMB}$ bằng:

• A. 30°;
• B. 45°;
• C. 60°;

• D. 90°.

Câu 33: Một hộp có 10 lá thăm có kích thước giống nhau và được đánh số từ 1 đến 10. Lấy ngẫu nhiên 1 lá thăm từ hộp. Tính xác suất của biến cố “Lấy được là thăm ghi số 9”.

• A. 0;
• B. $\frac{9}{10}$

• C. $\frac{1}{10}$

• D. 1.

Câu 34: Kết quả của phép tính (18$x^6$ + 6$x^4$ – 3$x^2$) : (3$x^2$) là

• A. 6$x^4$ + 2$x^2$ + 1;
• B. 6$x^4$ - 2$x^2$ + 1

• C. 6$x^4$ + 2$x^2$ - 1

• D. 6$x^4$ - 2$x^2$ - 1

Câu 35: Cho ∆ABC cân tại A. Gọi M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại E. Điểm E thuộc đường thẳng nào trong các đường thẳng sau đây.

• A. BC;

• B. AM;

• C. AB;
• D. AC.

Câu 36: Cho ∆ABC cân tại A. Gọi CP, BQ là các đường phân giác của ∆ABC (P ∈ AB, Q ∈ AC). Gọi O là giao điểm của CP và BQ. Cho các khẳng định sau:

(I) ∆OBC cân;

(II) O cách đều ba cạnh AB, AC, BC;

(III) AO là đường trung trực của đoạn thẳng BC;

(IV) CP = BQ;

(V) ∆APQ cân tại P.

Số khẳng định đúng là:

• A. 2;
• B. 3;

• C. 4;

• D. 5.

Câu 37: Kết quả của phép chia 0,5$x^5$ + 3,2$x^3$ – 2$x^2$ cho 0,25$x^n$, với n = 2.

• A. 2$x^3$ + 12,8x + 8;

• B. 2$x^3$ + 12,8x - 8;

• C. 2$x^3$ - 12,8x - 8;
• D. 2$x^3$ - 12,8x + 8;

Câu 38: Trước trận chung kết bóng đá World Cup năm 2010 giữa hai đội Hà Lan và Tây Ban Nha, để dự đoán kết quả người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Hà Lan, một hộp gần cờ Tây Ban Nha và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Tây Ban Nha thắng.

• A. $\frac{3}{10}$

• B. $\frac{1}{2}$

• C. $\frac{7}{10}$
• D. $\frac{9}{10}$

Câu 39: Cho ∆ABC có BD và CE lần lượt là các đường cao hạ từ B, C và BD = CE. Gọi H là giao điểm của BD và CE. Khẳng định nào sau đây sai?

• A. ∆ABC cân tại A;

• B. ∆ABC cân tại B;

• C. H là trực tâm của ∆ABC;
• D. AH là đường phân giác của ∆ABC.

Câu 40: Cho ∆ABC cân tại A, đường trung tuyến AM. Đường trung trực của AB cắt AM ở O. Biết OA = 4 cm. Tính OB và OC.

• A. OB = OC = 2 cm;

• B. OB = OC = 4 cm;

• C. OB = OC = 8 cm;
• D. OB = 2 cm; OC = 4 cm.