NỘI DUNG TRẮC NGHIỆM

Câu 1: Biểu đồ dưới đây biểu diễn số lượng học sinh lớp 7A, 7B có nhà nằm ở 4 hướng Đông, Tây, Nam, Bắc của trường học:

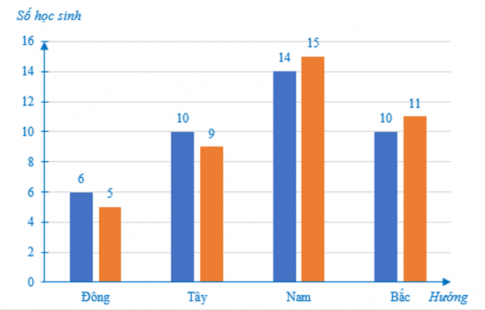
Một số bạn trong hai lớp 7A, 7B thường bị chói mắt do mặt trời chiếu thẳng vào mắt trong những ngày nắng vào những buổi sáng khi đi thẳng từ nhà đến trường. Hỏi có tất cả bao nhiêu bạn của hai lớp bị như vậy?

• A. 18 bạn;

• B. 19 bạn;

• C. 20 bạn;
• D. 21 bạn.

Câu 2: Quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của chuyển động rơi tự do được biểu diễn gần đúng bởi công thức y = 5x2. Người ta thả rơi tự do một vật nặng từ độ cao 200 m xuống đất. Hỏi khi vật nặng còn cách mặt đất 20 m thì nó đã rơi được thời gian bao lâu?

• A. 4 giây;
• B. 5 giây;

• C. 6 giây;

• D. 7 giây.

Câu 3: Xác định P(x) = a$x^2$ + bx + c biết P(1) = 0; P(–1) = 6 và P(2) = 3

• A. P(x) = 3x – 3;
• B. P(x) = –2$x^2$ – 3x + 5;

• C. P(x) = 2$x^2$ – 3x + 1;

• D. P(x) = 2$x^2$ – 3x – 1.

Câu 4: Cho biểu đồ biểu diễn tỉ lệ phần trăm loại nước uống yêu thích của học sinh lớp 7A.

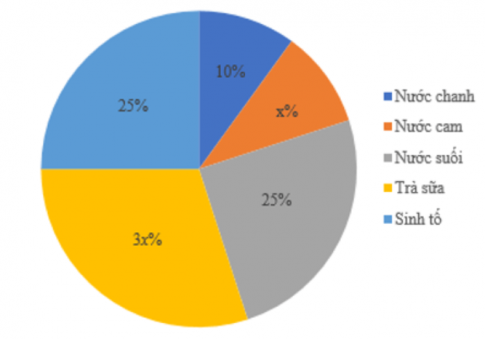
Tính giá trị của x.

• A. 5;

• B. 10;

• C. 15;
• D. 20.

Câu 5: Vòng tứ kết cuộc thi bơi lội có sáu trường với 8 học sinh đại diện tham gia:

- THCS Nguyễn Huệ: Kiệt

- THCS Nguyễn Khuyến: Long

- THCS Chu Văn An: Nguyên và Đăng

- THCS Nguyễn Bỉnh Khiêm: Minh

- THCS Lưu Văn Liệt: Thành

- THCS Nguyễn Du: Kha và Bình

Những kết quả thuận lợi cho biến cố “Người chiến thắng không phải đến từ trường THCS Nguyễn Du” là:

• A. Kiệt, Nguyên, Đăng, Thành, Long, Minh;

• B. Kiệt, Nguyên, Đăng, Thành, Long, Minh, Kha;
• C. Kiệt, Nguyên, Đăng, Thành, Long;
• D. Kha, Long, Nguyên, Đăng, Bình.

Câu 6: Cho biểu đồ nhiệt độ trung bình hàng tháng ở một tỉnh trong một năm:

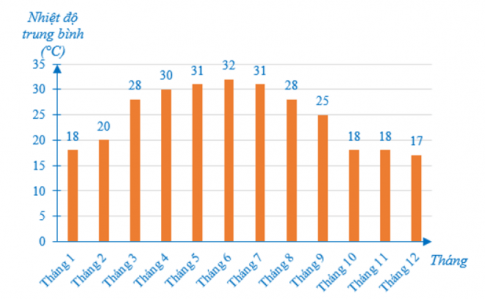
Khoảng thời gian nóng nhất năm là:

• A. Từ tháng 10 đến tháng 12;

• B. Từ tháng 4 đến tháng 7;
• C. Từ tháng 1 đến tháng 3;
• D. Từ tháng 7 đến tháng 10;

Câu 7: Cuối tuần, Trung được bố mẹ cho phép đến nhà Thành chơi nhưng con đường Trung thường đi đang sửa chữa nên Trung phải đi đường khác. Giữa đường có 4 ngã rẽ, nhưng chỉ có một ngã dẫn đến nhà Thành, Trung không nhớ cần rẽ ngã nào. Có mấy kết quả có thể khi Trung chọn ngã rẽ?

• A. 2 kết quả;

• B. 3 kết quả;
• C. 4 kết quả;
• D. Tất cả đều sai.

Câu 8: Một mảnh đất hình chữ nhật có kích thước chiều dài, chiều rộng lần lượt là 3x m và 2 m. Người ta dự định trồng hoa trong phần đất hình vuông có cạnh là x m như hình vẽ.

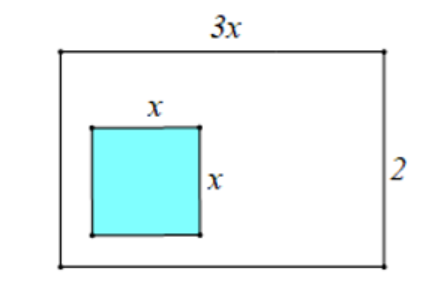
Diện tích phần đất còn lại (phần đất không tô màu) là:

• A. $x^2$ – 6x ($m^2$)
• B. 5$x^2$ ($m^2$)
• C. 6$x^2$ ($m^2$)

• D. 6x – $x^2$ ($m^2$)

Câu 9: Cho ∆ABC = ∆DEG biết $\widehat{A}$ + $\widehat{E}$ = 100°. Số đo góc G là:

• A. 50°;
• B. 60°;
• C. 70°;

• D. 80°.

Câu 10: Cho biểu đồ tỉ lệ thí sinh được trao huy chương các loại trong một cuộc thi.

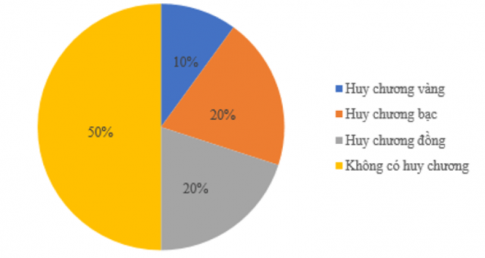
Hai loại huy chương nào có cùng tỉ lệ thí sinh được trao?

• A. Huy chương vàng và huy chương bạc;
• B. Huy chương vàng và huy chương đồng;

• C. Huy chương bạc và huy chương đồng;

• D. Không có hai loại nào có cùng tỉ lệ.

Câu 11: Khẳng định nào sau đây là sai khi nói về biểu đồ đoạn thẳng?

• A. Trục nằm ngang biểu diễn các đối tượng thống kê;
• B. Biểu đồ đoạn thẳng là đường gấp khúc nối từng điểm liên tiếp bằng các đoạn thẳng;
• C. Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định bởi một đối tượng thống kê và số liệu thống kê theo tiêu chí của đối tượng đó.

• D. Trục nằm ngang biểu diễn tiêu chí thống kê và trên trục đó đã xác định độ dài đơn vị thống kê.

Câu 12: Hệ số cao nhất và hệ số tự do của đa thức –7$x%5$ – 9$x^2$ + $x^6$ – $x^4$ + 10 lần lượt là:

• A. –7 và 10
• B. 10 và –7
• C. 10 và 1

• D. 1 và 10

Câu 13: Cho hai tam giác ABC và DEF như hình vẽ dưới đây:

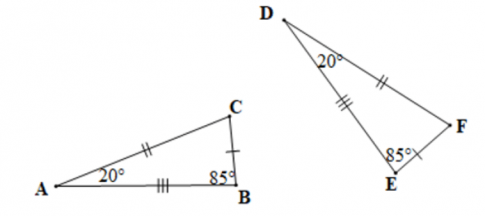
Khẳng định nào sau đây là đúng?

• A. $\Delta$ ABC = $\Delta$ DEF;

• B. $\Delta$ ABC = $\Delta$ DFE;
• C. $\Delta$ ABC = $\Delta$ EDF;
• D. $\Delta$ ABC = $\Delta$ FDE.

Câu 14: Cho hình vẽ sau:

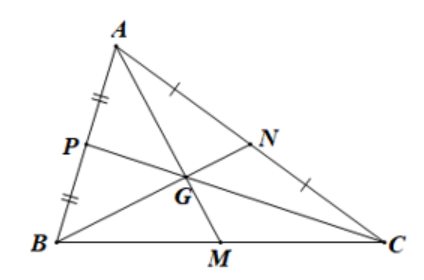
Biết AM = 3 cm. Độ dài đoạn thẳng GM là:

• A. 1 cm;

• B. 2 cm;
• C. 3 cm;
• D. 4,5 cm.

Câu 15: Một hộp có 12 quả bóng cùng màu, mỗi quả được ghi một trong các số 1, 2, 3, …, 12; hai quả khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một quả trong hộp. Xét biến cố “Số xuất hiện trên quả bóng được lấy ra là hợp số”. Kết quả thuận lợi cho biến cố trên là:

• A. 4, 6, 8, 9, 10, 12;

• B. 3, 4, 6, 8, 9, 12;
• C. 4, 5, 7, 8, 10, 11;
• D. 1, 2, 4, 6, 8, 12.

Câu 16: Cho biểu đồ đoạn thẳng biểu diễn chiều cao của một cây đậu trong 5 ngày.

Theo em, ngày thứ 5 chiều cao của cây đậu tăng bao nhiêu so với ngày thứ 4?

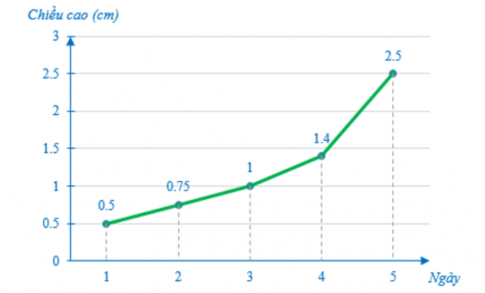
• A. 1,4 cm;
• B. 1,3 cm;
• C. 1,2 cm;

• D. 1,1 cm.

Câu 17: Biểu thức A = (x + 1)($x^2$+ 2) có bao nhiêu nghiệm?

• A. 0;

• B. 1;

• C. 2;
• D. 3.

Câu 18: Cho biết $\Delta$ ABC = ∆XYZ, AB = 4 cm, AC = 3 cm, BC = 6 cm. Độ dài cạnh XY là:

• A. 3 cm;

• B. 4 cm;

• C. 5 cm;
• D. 6 cm.

Câu 19: Cho ∆ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Hãy so sánh GX, GY và GZ.

• A. GX > GY > GZ;

• B. GX = GY = GZ;

• C. GX < GY = GZ;
• D. GX = GY > GZ.

Câu 20: Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = 5$x^4$ – 4$x^2$ + 6$x^3$ + x – 1; g(x) = 3 – 2x.

• A. –1;

• B. –5;

• C. 4;
• D. 6.

Câu 21: Tung ngẫu nhiên hai đồng xu cân đối. Trong các biến cố sau, biến cố nào không là biến cố ngẫu nhiên?

• A. “Số đồng xu xuất hiện mặt sấp không vượt quá 2";

• B. “Số đồng xu xuất hiện mặt sấp gấp 2 lần số đồng xu xuất hiện mặt ngửa”;
• C. “Có ít nhất một đồng xu xuất hiện mặt sấp”;
• D. “Số đồng xu xuất hiện mặt ngửa gấp 2 lần số đồng xu xuất hiện mặt sấp”.

Câu 22: Tỉ lệ tăng dân số Việt Nam trong một số năm gần đây được cho trong bảng sau:

Dựa vào biểu đồ biểu diễn bảng số liệu trên, tìm giá trị của x.

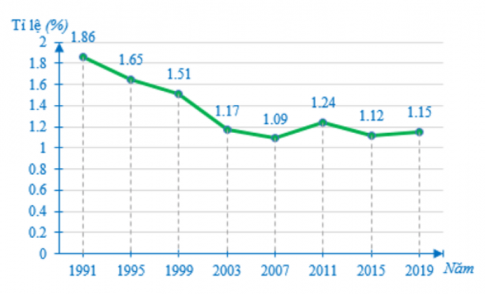
• A. 1,09;

• B. 1,17;
• C. 1,65;
• D. 1,51.

Câu 23: Cho ∆ABC = ∆PQR, biết BC = 4 cm. Cạnh nào của tam giác PQR có độ dài bằng 4 cm?

• A. QP;

• B. QR;

• C. PR;
• D. Không có cạnh nào.

Câu 24: Cho ∆ABC có đường trung tuyến AD. Trên đoạn thẳng AD lấy hai điểm E, G sao cho AG = GE = ED. Trọng tâm của ∆ABC là điểm:

• A. B;

• B. E;

• C. G;
• D. D.

Câu 25: Cho hai đa thức f(x) = 6$x^2$ + 4x – 5 và g(x) = –6$x^2$ – 4x + 2. Tính h(x) = f(x) + g(x) và tìm bậc của h(x).

• A. h(x) = 12$x^2$ + 8x – 7 và bậc của h(x) là 2;
• B. h(x) = –3 và bậc của h(x) là 1;
• C. h(x) = 8x – 3 và bậc của h(x) là 1;

• D. h(x) = –3 và bậc của h(x) là 0.

Câu 26: Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ. Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra?

• A. 5;

• B. 1, 2, 3, 4, 5;

• C. 1, 2, 3;
• D. 1, 2.

Câu 27: Cho đa thức P(x) = –6$x^5$ – 4$x^4$ + 3$x^2$ – 2x và Q(x) = 2$x^5$ – 4$x^4$ – 2$x^3$ + 2$x^2$ – x – 3. Tính M(1) với M(x) = P(x) – Q(x).

• A. –3;

• B. 3;
• C. –2;
• D. 2.

Câu 28: Biểu đồ dưới đây cho biết kỉ lục thế giới về thời gian chạy cự li 100 m trong các năm từ 1912 đến 2005:

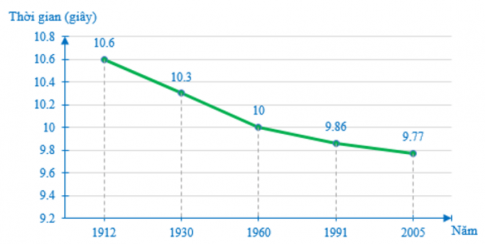
Từ năm 1912 đến 2005, kỉ lục thế giới về chạy cự li 100 m đã giảm được bao nhiêu giây?

• A. 0,81 giây;

• B. 0,83 giây;

• C. 0,85 giây;
• D. 0,87 giây.

Câu 29: Cho hai đa thức P(x) và Q(x) dưới đây, hai đa thức nào thỏa mãn P(x) – Q(x) = 2x – 2 là:

• A. P(x) = $x^2$ – 2x; Q(x) = –2x – 2;
• B. P(x) = $x^2$ – 2x; Q(x) = 2$x^2$ + 2x;
• C. P(x) = 2x; Q(x) = –2;

• D. P(x) = $x^3$ – 2; Q(x) = $x^3$ – 2x.

Câu 30: Cho ∆ABC đều có ba đường trung tuyến AD, BE, CF cắt nhau tại G. Đoạn thẳng BE bằng với đoạn thẳng nào trong các đoạn thẳng sau:

• A. AD;
• B. CF;
• C. AB;

• D. Cả A, B đều đúng.

Câu 31: Cho tam giác DEG (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh I, H, K. Biết $\widehat{D}$ = $\widehat{K}$, $\widehat{G}$ = $\widehat{I}$. Kí hiệu về sự bằng nhau của hai tam giác là:

• A. $\Delta$ DEG = $\Delta$ IHK;
• B. $\Delta$ DEG = $\Delta$ HIK;
• C. $\Delta$ DEG = $\Delta$ KIH;

• D. $\Delta$ DEG = $\Delta$ KHI.

Câu 32: Cho biểu đồ biểu diễn số vụ tai nạn giao thông (TNGT) của nước ta trong giai đoạn từ năm 2016 đến 2020:

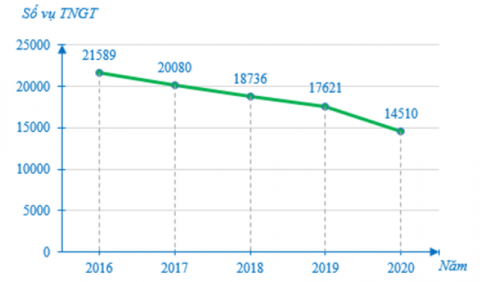
Số vụ TNGT năm 2020 đã giảm bao nhiêu phần trăm so với năm 2019 (làm tròn kết quả đến hàng phần mười)?

• A. 16,7%;

• B. 17,7%;

• C. 18,7%;
• D. 19,7%.

Câu 33: Gieo ngẫu nhiên xúc xắc một lần. Xét biến cố “Mặt xuất hiện có số chấm là số nguyên tố”. Những kết quả thuận lợi cho biến cố trên là:

• A. 1, 2, 3;

• B. 2, 3, 5;

• C. 2, 4, 6;
• D. 1, 3, 5.

Câu 34: Cho $\Delta$ ABC có hai đường trung tuyến BE và CF cắt nhau tại G. Biết BE = CF. Khẳng định nào sau đây đúng nhất?

• A. $\Delta$ BCG cân tại G;
• B. $\Delta$ ABC cân tại A;
• C. AG ⊥ BC;

• D. Cả A, B, C đều đúng.

Câu 35: Cho f(x) = 2$x^4$ – 4$x^2$ + 6$x^3$ + 2x + 3; g(x) = x + 3 và f(x) + k(x) = g(x). Hệ số tự do của đa thức k(x) là:

• A. –1;
• B. 4;

• C. 0;

• D. 6.

Câu 36: Cho biểu đồ biểu diễn tỉ lệ phần trăm loại nước uống yêu thích của học sinh lớp 7A.

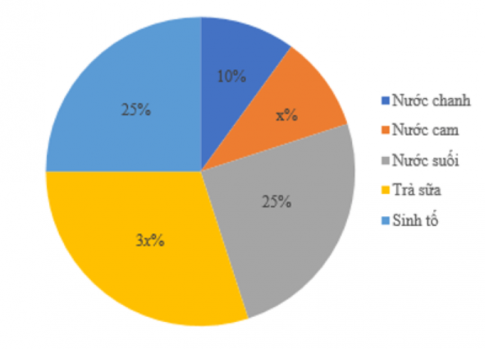
Tính giá trị của x.

• A. 5;

• B. 10;

• C. 15;
• D. 20.

Câu 37: Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, …, 12. Hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Những kết quả thuận lợi cho biến số “Số xuất hiện trên thẻ là số chia hết cho 3” là:

• A. 3, 6, 9, 12;

• B. 3, 6, 8, 12;
• C. 3, 5, 7, 9;
• D. 2, 4, 6, 8.

Câu 38: Cho $\Delta$ ABC = $\Delta$ HIK. Khẳng định nào sau đây là đúng?

• A. $\widehat{ABC}$ = $\widehat{IHK}$

• B. $\widehat{BCA}$ = $\widehat{HKI}$

• C. AB = HK;
• D. BC = HK.

Câu 39: Cho tam giác như hình vẽ dưới đây, có chu vi bằng 6x – 10.

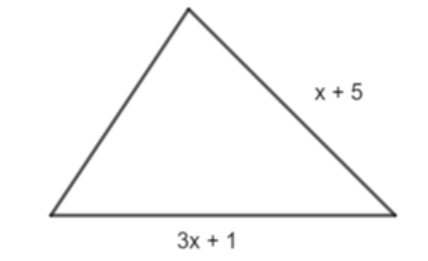
Độ dài cạnh chưa biết của tam giác trên là:

• A. 2x + 17;

• B. 2x – 17;

• C. 17x + 2;
• D. 17x – 2.

Câu 40: Gieo ngẫu nhiên ba đồng xu phân biệt một lần. Kí hiệu S, N lần lượt chỉ đồng xu lật mặt sấp, lật mặt ngửa. Những kết quả thuận lợi cho biến cố “Có ít nhất hai đồng xu xuất hiện mặt ngửa” là:

• A. NNS, NSN, SNN;

• B. NNS, NSN, SNN, NNN;

• C. N, N, S;
• D. N, N, N.