Video giảng Toán 11 kết nối Bài 15: Giới hạn của dãy số

Tóm lược nội dung

BÀI 15. GIỚI HẠN CỦA DÃY SỐ (3 TIẾT)

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

• Nhận biết khái niệm giới hạn của dãy số.
• Giải thích một số giới hạn cơ bản.
• Vận dụng các phép toán giới hạn để tìm giới hạn của một số dãy số đơn giản.
• Tính tổng của một cấp số nhân lùi vô hạn và vận dụng được kết quả đó để giải quyết một số tình huống thực tiễn giả định hoặc liên quan đến thực tiễn.

HOẠT ĐỘNG KHỞI ĐỘNG

Trước khi bước vào bài học ngày hôm nay, các em đọc phần Nghịch lý Zeno:

Achilles (nhân vật trong thần thoại Hy Lạp, được mô tả có thể chạy nhanh như gió) đuổi theo một con rùa trên một đường thẳng. Vị trí xuất phát của Achilles là , cách vị trí xuất phát  của rùa một quãng đường có chiều dài là a. Zeno lí luận rằng, mặc dù chạy nhanh hơn nhưng Achilles không bao giờ đuổi kịp rùa.

Thật vậy, trước tiên Achilles phải đến được vị trí  trong khoảng thời gian này, rùa đã di chuyển đến vị trí . Sau đó, Achilles phải đến được vị trí , lúc này rùa đã di chuyển đến vị trí  Cứ như vậy, Achilles không bao giờ đuổi kịp rùa.

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Nội dung 1: Giới hạn của dãy số.

Các em quan sát hình 4.13 và trả lời câu hỏi:

+ Khoảng cách từ một số a bất kì đến số  được gọi là gì của ?

+ Nếu cho 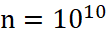 thì giá trị của  sẽ bằng bao nhiêu? Nếu biểu diễn trên trục số thì giá trị đó như thế nào với số 0?

(gần tiến tới 0).

Video trình bày nội dung:

Năm số hạng đầu của dãy số  đã cho là .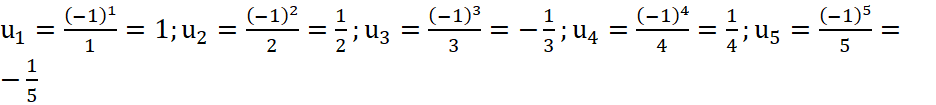

Biểu diễn các số hạng này trên trục số, ta được:

b) Khoảng cách từ  đến 0 là .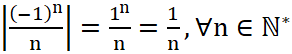

Ta có: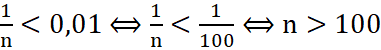

Vậy bắt đầu từ số hạng thứ 101 của dãy thì khoảng cách từ  đến 0 nhỏ hơn 0,01.

Ta nói dãy số  có giới hạn là 0 khi n dần tới dương vô cực, nếu  có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu  hay  khi .

Nội dung 2: Định lí về giới hạn hữu hạn của dãy số.

+ Em hãy tính  sau đó tính giới hạn của tổng .

+ Em hãy tính giới của  và  sau đó tính tổng hai giới hạn đó.

Video trình bày nội dung:

HĐ3.

+) Ta có: 

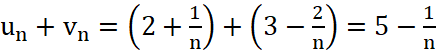
Lại có: 

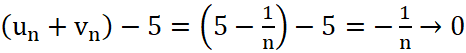khi

Do vậy,

+) Ta có: 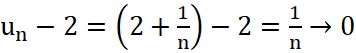 khi

 Do vậy ,

Và 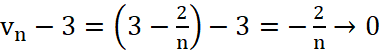 khi

Do vậy,

Khi đó,

Vậy

Quy tắc tính giới hạn

a) Nếu  và  thì

+

+

+

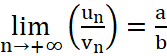+  (nếu ) 

b)  Nếu  với mọi n và  thì

và

………..

Nội dung video Bài 15: Giới hạn của dãy số còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.