Video giảng Toán 11 kết nối Bài 11: Hai đường thẳng song song

Tóm lược nội dung

BÀI 11. HAI ĐƯỜNG THẲNG SONG SONG (3 TIẾT)

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

• Nhận biết vị trí của hai đường thẳng trong không gian: hai đường thẳng trùng nhau, cắt nhau, song song và chéo nhau.
• Giải thích tính chất cơ bản của hai đường thẳng song song trong không gian: Qua một điểm nằm ngoài một đường thẳng cho trước có đúng một đường thẳng song song với đường thẳng đã cho; định lí ba đường giao tuyến.
• Nhận biết một vài tính chất của hai đường thẳng song song và biết áp dụng để giải một số bài tập đơn giản. Các tính chất thừa nhận bao gồm: hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau; hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó, hoặc trùng với một trong hai đường thẳng đó.
• Mô tả và giải thích một số hình ảnh thực tiễn có liên quan đến vị trí tương đối của hai đường thẳng trong không gian.

HOẠT ĐỘNG KHỞI ĐỘNG

Trước khi bước vào bài học ngày hôm nay, các em đọc tình huống mở đầu: Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Nội dung 1: Vị trí tương đối của hai đường thẳng

Theo em:

+Tất cả những câu hỏi và đáp án mà các em vừa thực hiện trong HĐ1 đều nói đến những vị trí của hai đường thẳng trong không gian. Nó được gọi là vị trí tương đối của hai đường thẳng trong không gian. Vậy trong không gian có 2 đường thẳng có những vị trí tương đối nào?

+ Nếu đường thẳng  và  song song thì có bao nhiêu mặt phẳng chứa  và ?

Video trình bày nội dung:

Cho hai đường thẳng a và b trong không gian.

• Nếu  và  cùng nằm trong một mặt phẳng thì ta nói  và  đồng phẳng. Khi đó,  và  có thể cắt nhau, song song với nhau hoặc trùng nhau.

• Nếu  và  không cùng nằm trong bất kì mặt phẳng nào thì ta nói  và  chéo nhau. Khi đó, ta cũng nói  chéo với , hoặc  chéo với .

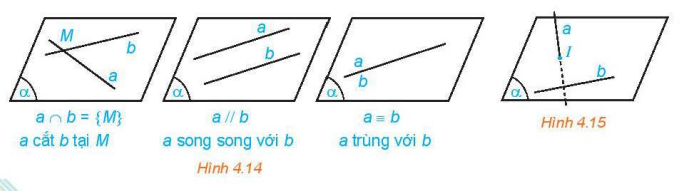
- Hai đường thẳng song song là hai đường thẳng đồng phẳng và không có điểm chung.

- Có đúng một mặt phẳng chứa hai đường thẳng song song.

Nội dung 2: Tính chất của hai đường thẳng song song

+ Các em hãy nhớ lại kiến thức trong hình học phẳng rằng có bao nhiêu đường thẳng đi qua một điểm và song song với một đường thẳng cho trước? Hãy áp dụng điều đó để xử lý phần HĐ2.

+ Em hãy nêu định lí về ba đường giao tuyến.

Video trình bày nội dung:

Định lí về ba đường giao tuyến

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy hoặc đôi một song song với nhau.

………..

Nội dung video Bài 11: Hai đường thẳng song song còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.