Giải Câu 4 Bài: Ôn tập cuối năm Phần Hình học sgk Toán 8 tập 2 Trang 132
Câu 4: Trang 132 - SGK Toán 8 tập 2
Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm của BN và CM. Hình bình hành ABCD phải có điều kiện gì để tứ giác MENK là:
a) Hình thoi?
b) Hình chữ nhật?
c) Hình vuông?
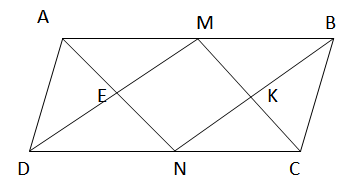
Tứ giác MBND là hình bình hành.
(MB// = ND)
Lại có MN // BC (vì MBCN là hình bình hành).
EK // CD (vì EK là đường trung bình của ∆CDM).
a) Để MENK là hình thoi thì hình bình hành MENK phải có hai đường chéo vuông góc. Tức là MN ⊥ EK.
Suy ra BC ⊥ CD.
Vậy ABCD phải là hình chữ nhật.
b) Để MENK là hình chữ nhật thì hình bình hành MENK phải có hai đường chéo bằng nhau. Tức là MN = EK.
Mà MN = BC, EK = \({1 \over 2}CD\) suy ra:
BC = \({1 \over 2}\) CD.
c) Để MENK là hình vuông thì MENK phải vừa là hình thoi vừa là hình chữ nhật. Tức là hình bình hành ABCD phải là hình chữ nhật có:
BC = \({1 \over 2}DC\)

Bình luận