Giải Câu 2 Bài: Ôn tập cuối năm Phần Hình học sgk Toán 8 tập 2 Trang 131

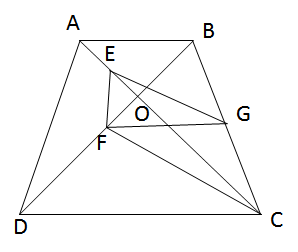
Tam giác ABO đều nên tam giác CDO cũng đều, suy ra OD = OC.

∆AOD = ∆BOC (c.g.c) =>AD = BC.

EF là đường trung bình của tam giác AOD nên:

 (1) \(EF = {1 \over 2}AD = {1 \over 2}BC\)   (1)

CF là đường trung tuyến của tam giác đều CDO nên CF ⊥ DO, nghĩa là .Trong tam giác vuông CFB, FG là đường trung tuyến ứng với cạnh huyền nên:

 (2) \(FG = {1 \over 2}BC\)

Chứng minh tương tự ta cũng có:

 (3) \(EG = {1 \over 2}BC\)

Từ (1), (2), (3) suy ra EF = GF = EG nên tam giác EFG là tam giác đều.