Đáp án câu 5 đề 2 kiểm tra học kì II toán 8
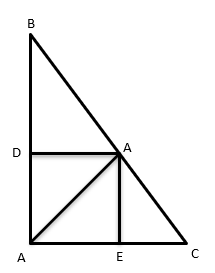
5. Cho tam giác $ABC$ vuông tại $A$ có $AH$ là đường cao. Vẽ $HD ⊥ AB ( D ∈ AB )$. $HE ⊥ AC ( E ∈ AC )$. $AB = 12$cm, $AC = 16 $cm
a) Chứng minh : $ΔHAC ∼ ΔABC$
b) Chứng minh : $AH^{2}$ = $AD.AB$
c) Chứng minh : $AD.AB = AE.AC$.
d) Tính $\frac{S_{ADE}}{S_{ABC}}$
5. 
a) Xét $ΔHAC$ và $ΔABC$ có:
$\widehat{ACH}$ là góc chung
$\widehat{BAC}$= $\widehat{AHC}$ = $90^{\circ}$
⇒ $ΔHAC ∼ ΔABC$ (g.g)
b) Xét $ΔHAD$ và $ΔBAH$ có:
$\widehat{DAH}$ là góc chung
$\widehat{ADH}$ = $\widehat{AHB}$ = $90^{\circ}$
⇒ $ΔHAD ∼ ΔBAH$ (g.g)
$\Rightarrow $ $\frac{AH}{AB} $ = $\frac{AD}{AH} $ $\Rightarrow $ $AH^{2}$ = $AB.AD$
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ $ΔADH= ΔAEH$ ( c.c.c) ⇒ $\widehat{DHA}$= $\widehat{DEA}$
Mặt khác: $ΔHAD ∼ ΔBAH$ ⇒ $\widehat{DHA}$= $\widehat{BAH}$
$\widehat{BAH}$= $\widehat{DEA}$
Xét $ΔEAD$ và $ΔBAC$ có:
$\widehat{DHA}$= $\widehat{DEA}$
$\widehat{DEA}$ là góc chung
ΔEAD ∼ ΔBAC (g.g)
$\Rightarrow $ $\frac{EA}{BA}$ = $\frac{AD}{AC}$ $\Rightarrow $ $AD.AB$ = $AE.AC$
d) $ΔEAD$ ∼ $ΔBAC$
$\Rightarrow $ $\frac{S_{ADE}}{S_{ABC}}$ = $\left ( \frac{AD}{AC} \right )^{2}$
$ΔABC$ vuông tại A, theo định lí Pytago:
$BC$ = $\sqrt{AB^{2} + AC^{2}}$ = $\sqrt{12^{2} + 16^{2}}$ = $20$
Mặt khác, ta có: $S_{ABC}$ = $\frac{1}{2}AB.AC$ = $\frac{1}{2}.AH.BC$
$\Rightarrow $ $AH$ = $\frac{AB.AC}{BC}$ = $\frac{12.16}{20}$ = $\frac{48}{5}$
Theo b, ta có:
$AH^{2}$ = $AB.AD$ $\Rightarrow $ $AD$ = $\frac{AH^{2}}{AB}$ = $\frac{\left ( \frac{48}{5} \right )^{2}}{12}$ = $\frac{192}{25} $
$\frac{S_{ADE}}{S_{ABC}}$ = $\left ( \frac{AD}{AC} \right )^{2}$ = $\left ( \frac{\frac{192}{25}}{16} \right )^{2}$
Xem toàn bộ: Toán 8: Đề kiểm tra kì II (Đề 2)

Bình luận