BÀI TẬP CUỐI CHƯƠNG I

BÀI TẬP TRẮC NGHIỆM

Bài tập 1: Góc lượng giác nào tương ứng với chuyển động quay 3 vòng ngược chiều kim đồng hồ?

A.

B. ⁰

C. 1152^o

D. 1152π

Đáp án chuẩn:

C. 

Bài tập 2:Trong trường hợp nào dưới đây cosα = cosβ và sinα = – sinβ ?

A. β = – α

B. β = π – α

C. β = π + α

D. β = + α

Đáp án chuẩn:

A.

Bài tập 3: Khẳng định nào sau đây đúng?

A. Hàm số y = sinx là hàm số chẵn

B. Hàm số y = cosx là hàm số chẵn

C. Hàm số y = tanx là hàm số chẵn

D. Hàm số y = cotx là hàm số chẵn

Đáp án chuẩn:

B.

Bài tập 4 : Nghiệm âm lớn nhất của phương trình lượng giác cos2x = cos là?

A.

B.

C.

D.

Đáp án chuẩn:

A. 

Bài tập 5: Số nghiệm của phương trình tanx = 3 trong khoảng (; ) là

A. 1

B. 2

C. 3

D. 4

Đáp án chuẩn:

B. 

Bài tập 6: Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức h(t) = 29 + 3sin(t-9), với h được tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ

A. 32°C, lúc 15 giờ

B. 29°C, lúc 9 giờ

C. 26°C, lúc 3 giờ

D. 26°C, lúc 0 giờ

Đáp án chuẩn:

C

BÀI TẬP TỰ LUẬN

Bài tập 7 ; Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian?

Đáp án chuẩn:

Bài tập 8: Cho cosα = Và <<0. Tính:

a) sinα;

b) sin2α;

c) cos(α+)

Đáp án chuẩn:

a) ;

b) ;

c)

Bài tập 9: Chứng minh đẳng thức lượng giác:

a) sin(α + β)sin(α – β) = sin2α – sin2β

b) = Cos2

Đáp án chuẩn:

a)

b)

Bài tập 10: Nghiệm dương nhỏ nhất của phương trình là bao nhiêu?

Đáp án chuẩn:

Bài tập 11: Giải các phương trình sau:

a) sin2x + cos3x = 0;

b) sinxcosx =

c) sinx + sin2x = 0

Đáp án chuẩn:

a)

b

c)

Bài tập 12: Độ sâu h(m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thủy triều lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức h(t) = 0,8cos0,5t + 4

a) Độ sâu của nước vào thời điểm t = 2 là bao nhiêu mét?

b) Một con tàu cần mực nước sâu tối thiểu 3,6m để có thể di chuyển vào cảng an toàn. Dựa vào đồ thị của hàm số cosin, hãy cho biết trong vòng 12 tiếng sau khi thủy triều lên lần đầu tiên, ở những thời điểm t nào tàu có thể hạ thủy. Làm tròn kết quả đến hàng phần trăm.

Đáp án chuẩn:

a)

b) thuộc hoặc (giờ)

Bài tập 13: Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được cho bởi công thức v = -3sin

(Theo https://www.britannica.com/science/simple-harmonic-motion)

Xác định các thời điểm t mà tại đó:

a) Vận tốc con lắc đạt giá trị lớn nhất;

b) Vận tốc con lắc bằng 1,5 cm/s.

Đáp án chuẩn:

a) t

b) hoặc  

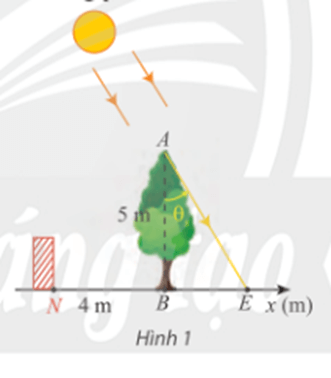
Bài tập 14; Trong Hình 1, cây xanh AB nằm ở trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5m. Bóng của cây là BE. Vào nghày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Góc thiên đỉnh θs = (AB, AE) phụ thuộc vào vị trí của Mặt Trời và thay đổi theo thời gian trong ngày theo công thức θs(t) = rad với t là thời gian trong ngày (theo đơn vị giờ, 6 < t < 18)

a) Viết hàm số biểu diễn tọa độ của điểm E trên trục Bx theo t.

b) Dựa vào đồ thị của hàm số tang, hãy xác định các thời điểm mà tại đó bóng cây phủ qua vị trí tường rào N biết N nằm trên trục Bx với tọa độ xN = – 4 (m). Làm tròn kết quả đến hàng phần mười.

Đáp án chuẩn:

a)

b) Trong khoảng từ 6 giờ đến khoảng 9,3 giờ thì bóng cây phủ qua vị trí tường rào