CHƯƠNG VIII: QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN

BÀI 5. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG. GÓC NHỊ DIỆN

CÂU HỎI MỞ ĐẦU

Mặt phẳng nghiêng thường được sử dụng trong lao động vì tính tiện dụng của nó. Quan sát hình mặt phẳng nghiêng (P) và mặt đất (Q) trong hình dưới đây và tìm hiểu tại sao:

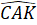• được gọi là góc hợp bởi đường thẳng d và (Q)
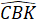• được gọi là góc hợp bởi hai mặt phẳng (P) và (Q)

Đáp án chuẩn: 

• K là hình chiếu vuông góc của C lên (Q)

• (P)∩(Q), CB⊥AB, BK⊥AB 

1. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

Khám phá 1: Cho đường thẳng a và mặt phẳng (P)

a) Trong trường hợp a vuông góc với (P), tìm góc giữa a và một đường thẳng b tuỳ ý trong (P)

b) Trong trường hợp a không vuông góc với (P), tìm góc giữa a và đường thẳng a' là hình chiếu vuông góc của a trên (P)

Đáp án chuẩn: 

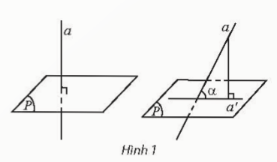
a) góc giữa và đường thẳng là góc vuông.

b) góc giữa và là góc .

Thực hành 1: Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa các đường thẳng sau đây với mặt phẳng (ABCD)

a) AA'

b) BC'

c) A'C

Đáp án chuẩn: 

a) .

b) .

c) .

Vận dụng 1: Một tấm ván hình chữ nhật ABCD được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết AB = 1 m, AB = 3,5 m. Tính góc giữa đường thẳng BD và đáy hố.

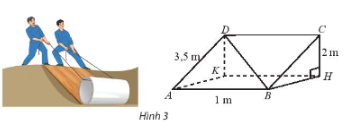
Đáp án chuẩn: 

góc giữa đường thẳng và đáy hồ khoảng .

2. GÓC NHỊ DIỆN VÀ GÓC PHẲNG NHỊ DIỆN

Khám phá 2: Cho hai đường thẳng (P) và (Q) cắt nhau theo giao tuyến d. Hãy gọi tên các nửa mặt phẳng có chung bờ d. Các nửa mặt phẳng này chia không gian thành bao nhiêu phần?

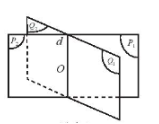
Đáp án chuẩn: 

Các nửa mặt phẳng này chia không gian thành 4 phần.

Khám phá 3: Cho góc nhị diện [P1,d,Q1]. Gọi O là một điểm tuỳ ý trên d, Ox là tia nằm trong (P1) và vuông góc với d, Oy là tia nằm trong (Q1) và vuông góc với d (Hình 6)

a) Nêu nhận xét về vị trí tương đối giữa d và mp(Ox, Oy)

b) Nêu nhận xét về số đo của góc xOy khi O thay đổi trên d

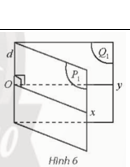
Đáp án chuẩn: 

a) .

b) Số đo của không đổi khi thay đổi trên .

Thực hành 2: Cho hình chóp tứ giác đều S.ABCD với O là tâm của đáy và có tất cả các cạnh đều bằng a. Xác định và tính góc phẳng nhị diện:

a) [S, BC, O]

b) [C, SO, B]

Đáp án chuẩn: 

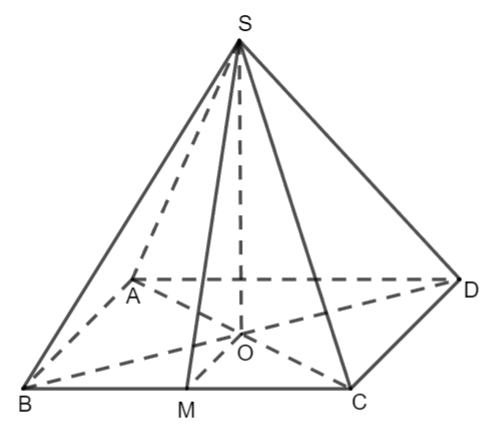
a) góc phẳng nhị diện của góc nhị diện

b) góc phẳng nhị diện của góc nhị diện =

Vận dụng 2: Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.

Đáp án chuẩn: 

góc là một góc phẳng của nhị diện

BÀI TẬP

Bài tập 1: Cho tứ diện đều ABCD, Vẽ hình bình hành BCED

a) Tìm góc giữa đường thẳng AB và (BCD)

b) Tìm góc phẳng nhị diện [A,CD,B]; [A,CD,E] 

Đáp án chuẩn: 

a)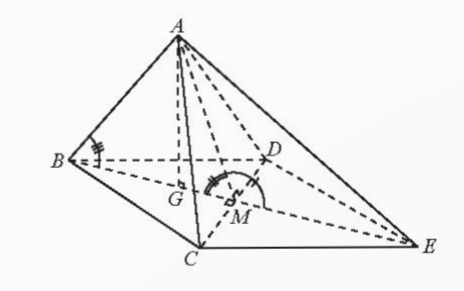

b) là góc phẳng nhị diện của góc nhị diện

Bài tập 2: Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và có tất cá các cạnh bằng nhau.

a) Tìm góc giữa đường thẳng SA và (ABCD)

b) Tìm góc phẳng nhị diện [A, SO, B], [S, AB, O] 

Đáp án chuẩn: 

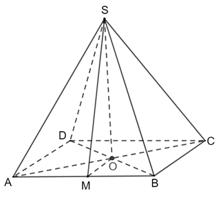
a) .

b)

  là góc phẳng nhị diện của góc nhị diện

Bài tập 3: Cho hình chóp cụt lục giác đều ABCDEF.A'B'C'D'E'F' với O và O' là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và a/2; OO' = a

a) Tìm góc giữa cạnh bên và mặt đáy

b) Tìm góc phẳng nhị diện [O, AB, A'], [O', A'B; A]

Đáp án chuẩn: 

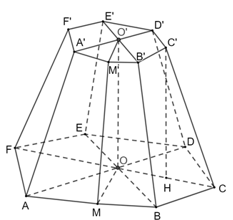
a) .

b) là góc phẳng nhị diện của , là góc phẳng nhị diện của

Bài tập 4: Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9

a) Tính số đo góc giữa đường thẳng CA' và (CC'B'B)

b) Tính số đo góc nhị diện cạnh CC'                                

Đáp án chuẩn: 

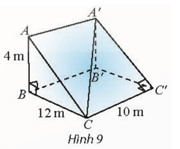
a) .

b) là góc phẳng nhị diện của góc nhị diện

Bài tập 5: Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135^o. Tính số mét khối cần di chuyển ra khỏi hầm

Đáp án chuẩn: 

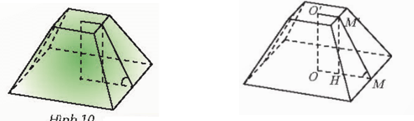
đất