BÀI 1. ĐIỂM, ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

1. MẶT PHẲNG TRONG KHÔNG GIAN

KP1: Mặt bàn, mặt bảng cho ta hình ảnh của mặt phẳng. Hãy chỉ thêm các ví dụ khác về hình ảnh một phần của mặt phẳng.

Đáp án chuẩn:

Mặt tivi, trang giấy, mặt gương,..

TH1: 

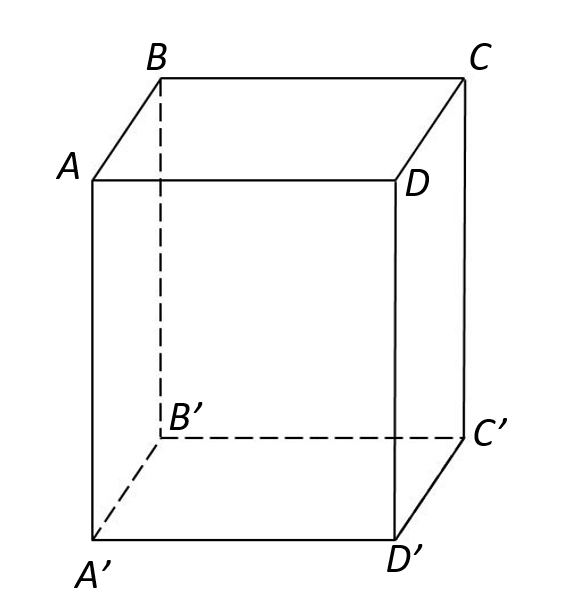
a) Vẽ hình biểu diễn của một hình hộp chữ nhật

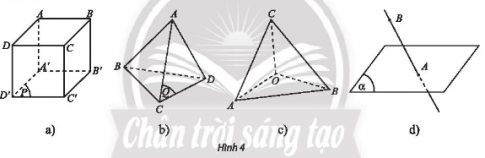
b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng (P)

c) Quan sát Hình 4b và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng (Q)

Đáp án chuẩn:

a) 

b) Điểm thuộc mặt phẳng (P) là: A'; B'; C'; D'

Điểm không thuộc mặt phẳng (P) là: A; B; C; D

c) Điểm thuộc mặt phẳng (Q) là: A; C; D

Điểm không thuộc mặt phẳng (Q) là: B

2. CÁC TÍNH CHẤT ĐƯỢC THỪA NHẬN CỦA HÌNH HỌC KHÔNG GIAN

KP2: Quan sát Hình 5 và cho biết muốn gác một cây sào tập nhảy cao, người ta cần dựa nó vào mấy điểm trên hai cọc đỡ.

Đáp án chuẩn:

Hai điểm trên hai cọc đỡ

TH2: Cho bốn điểm A, B, C, D phân biệt, trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu đường thẳng đi qua hai trong bốn điểm đã cho.

Đáp án chuẩn:

6 đường thẳng đi qua 2 trong 4 điểm

KP3: Quan sát Hình 7 và cho biết giá đỡ của máy ảnh tiếp đất tại mấy điểm. Tại sao giá đỡ máy ảnh thường có ba chân?

Đáp án chuẩn:

Vì khi đó giá đỡ tiếp đất tại 3 điểm

TH3: Có bao nhiêu mặt phẳng đi qua ba đỉnh của tam giác MNP?

Đáp án chuẩn:

1 mặt phẳng

KP4: Quan sát Hình 10 và cho biết thợ mộc kiểm tra mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào?

Đáp án chuẩn:

Người thợ mộc rê thước trên mặt bàn. Khi đó, nếu rê thước mà có 1 điểm thuộc cạnh thước nhưng không thuộc mặt bàn thì bàn đó chưa phẳng.

TH4: Cho mặt phẳng (Q) đi qua bốn đỉnh của tứ giác ABCD. Các điểm nằm trên đường chéo của tứ giác ABCD có thuộc mặt phẳng (Q) không? Giải thích.

Đáp án chuẩn:

Mặt phẳng (Q) là mặt phẳng duy nhất đi qua bốn điểm A, B, C, D.

Mọi điểm nằm trên đường chéo AC và BD đều thuộc mặt phẳng (Q)

KP5: Quan sát Hình 13 và cho biết bốn đỉnh A, B, C, D của cái bánh giò có cùng nằm trên một mặt phẳng hay không?

Đáp án chuẩn:

Không cùng nằm trên một mặt phẳng

TH5: Cho tam giác MNP và cho điểm O không thuộc mặt phẳng chứa ba điểm M, N, P. Tìm các mặt phẳng phân biệt được xác định từ bốn điểm M, N, P, O.

Đáp án chuẩn:

(OMN), (ONP), (OPM), (MNP)

KP6: Quan sát Hình 14 và mô tả phần giao nhau của hai bức tường.

Đáp án chuẩn:

Phần giao nhau là một đường thẳng

TH6: Cho A, B, C cùng thuộc một giao tuyến của hai mặt phẳng phân biệt 

( A,B,C thẳng hàng với nhau.

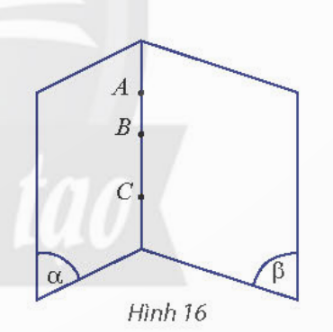
Đáp án chuẩn:

Vì A, B, C cùng nằm trên giao tuyến của hai mặt phẳng (α) và (β) 

=> A, B, C thẳng hàng

KP7: Trong mặt phẳng (P), cho tam giác ABC có M, N lần lượt là trung điểm của các đoạn thẳng AB, AC (Hình 17). Tính tỉ số

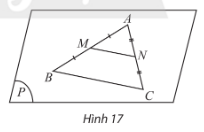
Đáp án chuẩn:

VD1: Tại sao muốn cánh cửa đóng mở được êm thì các điểm gắn bản lề A, B, C của cánh cửa và mặt tường (Hình 19) phải cùng nằm trên một đường thẳng?

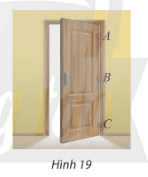
Đáp án chuẩn:

Nếu 3 điểm đều nằm trên cùng một đường thẳng thì đường thẳng đó chính là giao tuyến của hai mặt phẳng là mặt phẳng chứa cánh cửa và mặt phẳng chứa bức tường.

3. CÁCH XÁC ĐỊNH MẶT PHẲNG

KP8: Cho đường thẳng a và điểm A không nằm trên a. Trên a lấy hai điểm B, C. Đường thẳng a có nằm trong mặt phẳng (ABC) không? Giải thích.

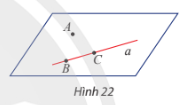
Đáp án chuẩn:

Đường thẳng a nằm trong mặt phẳng (P). 

KP9: Hai đường thẳng phân biệt a và b cắt nhau tại điểm O. Trên a, b lấy lần lượt hai điểm M, N khác O. Gọi (P) là mặt phẳng đi qua ba điểm M, N, O (Hình 25). Mặt phẳng (P) có chứa cả hai đường thẳng a và b không? Giải thích.

Đáp án chuẩn:

Đường thẳng a và b nằm trong mặt phẳng (P) vì:

+ (P) đi qua hai điểm N, O nên (P) chứa đường thẳng a.

+ (P) đi qua hai điểm M, O nên (P) chứa đường thẳng b.

TH7: Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b).

a) Tìm giao tuyến của hai mặt phẳng (M, a) và (M, b).

b) Lấy A, B lần lượt là hai điểm trên a, b và khác với điểm O. Tìm giao tuyến của (MAB) và mp(a, b).

c) Lấy điểm A’ trên đoạn MA và điểm B’ trên đoạn MB sao cho đường thẳng A’B’ cắt mp(a, b) tại C. Chứng minh ba điểm A, B, C thẳng hàng.

Đáp án chuẩn:

a) MO là giao tuyến cần tìm

b) AB là giao tuyến cần tìm

c)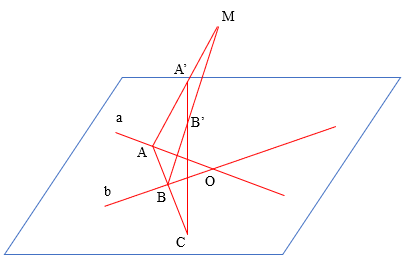

Giao tuyến của mặt phẳng (MAB) và mp(a,b) là AB

Mà C là giao của A’B’ với (a,b) nên C cũng thuộc giao tuyến của hai mặt phẳng (MAB) và (a,b).

=> A, B, C thẳng hàng

VD2: Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.

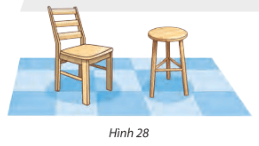
Đáp án chuẩn:

 Vì qua ba điểm không thẳng hàng có một và chỉ một mặt phẳng. Bốn điểm thì có thể không cùng nằm trên một mặt phẳng

VD3: Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser OA và OB của các mặt tường trong Hình 29.

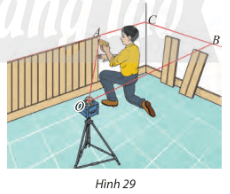
Đáp án chuẩn:

AC và BC

4. HÌNH CHÓP VÀ HÌNH TỨ DIỆN

KP10:

a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?

b) Tìm điểm giống nhau của các hình trong Hình 31.

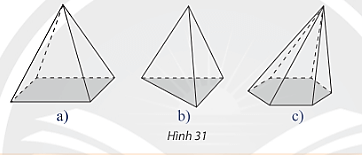
Đáp án chuẩn:

a) Hình tam giác

b) Các mặt bên đều là tam giác và có chung đỉnh

KP11: Trong Hình 34, hình chóp nào có số mặt ít nhất?

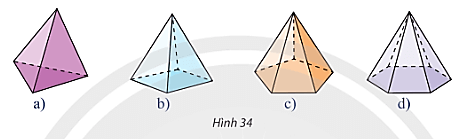
Đáp án chuẩn:

Hình 34a

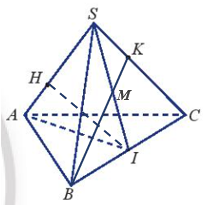
TH8: Cho tứ diện SABC. Gọi H, K lần lượt là hai điểm trên hai cạnh SA và SC (H ≠ S, A; K ≠ S, C) sao cho HK không song song với AC. Gọi I là trung điểm của BC (Hình 38).

a) Tìm giao điểm của đường thẳng HK và mặt phẳng (ABC).

b) Tìm giao tuyến của các mặt phẳng (SAI) và (ABK); (SAI) và (BCH).

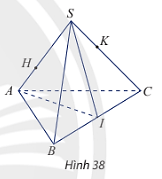
Đáp án chuẩn:

a) Giao điểm của đường thẳng HK và mặt phẳng (SAC) là E.

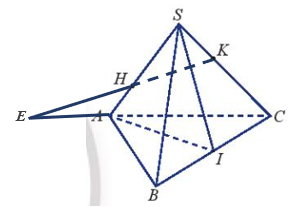
b) Giao tuyến của (SAI) và (ABK) là AM; Giao tuyến của (SAI) và (BCH) là HI.

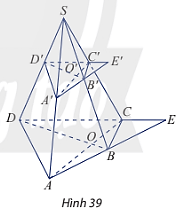
VD4: Cho hình chóp S.ABCD. Trên các cạnh bên của hình chóp lấy lần lượt các điểm A’, B’, C’, D’. Cho biết AC cắt BD tại O, A’C’ cắt B’D’ tại O’, AB cắt CD tại E và A’B’ cắt D’C’ tại E’ (Hình 39). Chứng minh rằng:

a) S, O’, O thẳng hàng;

b) S, E’, E thẳng hàng.

Đáp án chuẩn:

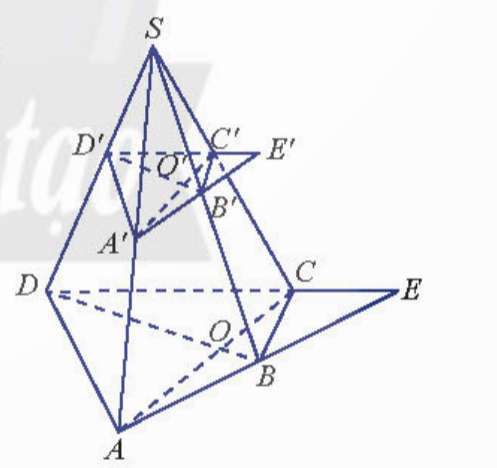
a) Giao tuyến của (SAC) và (SBD) là SO; Giao tuyến của (SA'C') và (SB'D') là SO'

Mà nên

Hay S, O, O' thẳng hàng

b) Giao tuyến của (SAB) và (SCD) là SE; Giao tuyến của (SA'B') và (SC'D') là SE'

Mà nên S

Hay S, E, E' thẳng hàng

VD5: Nêu cách tạo lập tứ diện đều SABC từ tam giác đều SS’S’’ theo gợi ý ở Hình 40.

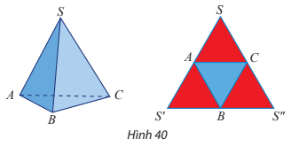
Đáp án chuẩn:

Gấp theo các cạnh AB, BC, CA để ba điểm S, S’, S’’ trùng nhau

BÀI TẬP CUỐI SGK

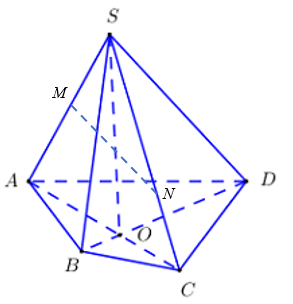
Bài tập 1: Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Lấy M, N lần lượt thuộc các cạnh SA, SC.

a) Chứng minh đường thẳng MN nằm trong mặt phẳng (SAC).

b) Chứng minh O là điểm chung của hai mặt phẳng (SAC) và (SBD).

Đáp án chuẩn:

a) Ta có: ; => nằm trong mặt phẳng .
b) Điểm thuộc và , suy ra là điểm chung của hai mặt phẳng và

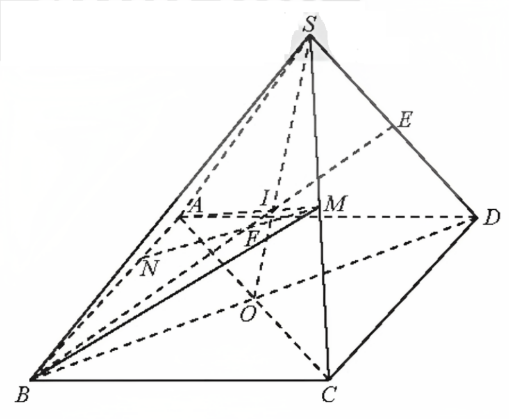
Bài tập 2: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC.

a) Tìm giao điểm I của đường thẳng AM và mặt phẳng (SBD). Chứng minh IA = 2IM.

b) Tìm giao điểm E của đường thẳng SD và mặt phẳng (ABM).

c) Gọi N là một điểm tùy ý trên cạnh AB. Tìm giao điểm của đường thẳng MN và mặt phẳng (SBD).

Đáp án chuẩn:

a) là trọng tâm của nên
b) Trong mặt phẳng , vẽ giao điểm của và

c) Trong mặt phẳng , vẽ giao điểm của và

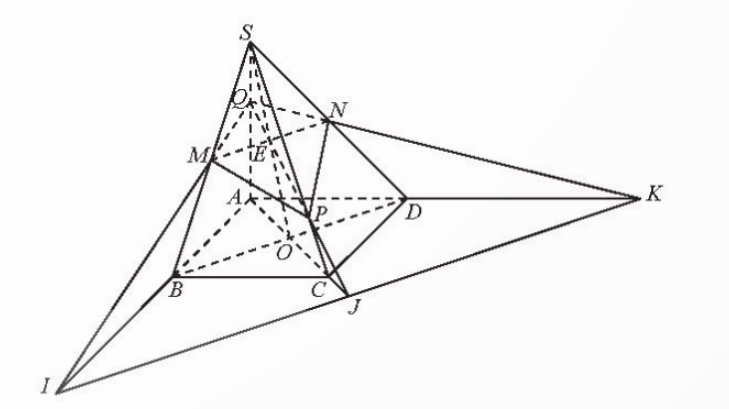
Bài tập 3: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD; M và N lần lượt là trung điểm của SB và SD; P thuộc đoạn SC và không là trung điểm của SC.

a) Tìm giao điểm E của đường thẳng SO và mặt phẳng (MNP).

b) Tìm giao điểm Q của đường thẳng SA và mặt phẳng (MNP).

c) Gọi I, J, K lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Chứng minh I, J, K thẳng hàng.

Đáp án chuẩn:

a) Trong mặt phẳng (SBD), vẽ giao điểm của và
b) Trong mặt phẳng , vẽ giao điểm của và
c) là ba điểm chung của và suy ra thẳng hàng

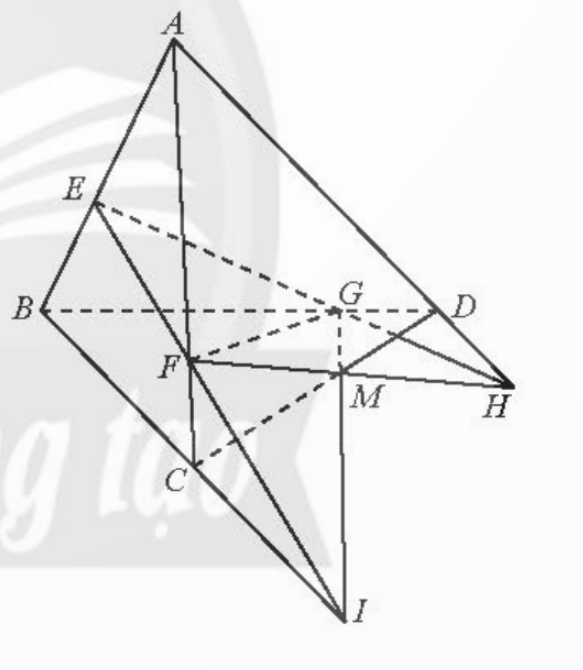
Bài tập 4: Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D).

a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) và (ACD).

b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm.

Đáp án chuẩn:

a) .
b) Trong mặt phẳng , vẽ giao điểm của và . 

Ta có là điểm chung của hai mặt phẳng và

=> Giao tuyến của hai mặt phẳng và phải đi qua . 

Như vậy cùng đi qua một điểm

Bài tập 5: Thước laser phát tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình 41). Giải thích tại sao các thước kẻ laser lại giúp người thợ xây dựng được đường thẳng trên tường hoặc sàn nhà.

Đáp án chuẩn:

Giao tuyến của mặt phẳng ánh sáng với mặt tường hoặc mặt sàn là một đường thẳng