BÀI 3. HAI MẶT PHẲNG VUÔNG GÓC

1. GÓC GIỮA HAI MẶT PHẲNG

Bài 1: a) Có thể xác định góc giữa hai cánh cửa nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?

b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại đo được góc giữa mặt phẳng nghiêng (Q) là mặt đất (P).

Đáp án chuẩn:

a) Có thể 

b) Thiết bị có thể đo được góc giữa hai dây dọi vuông góc với mặt nghiêng và mặt đất

2. HAI MẶT PHẲNG VUÔNG GÓC

Bài 1: Từ một điểm O vẽ hai tia Ox và Oy lần lượt vuông góc với hai bức tường trong phòng. Đo góc xOy 

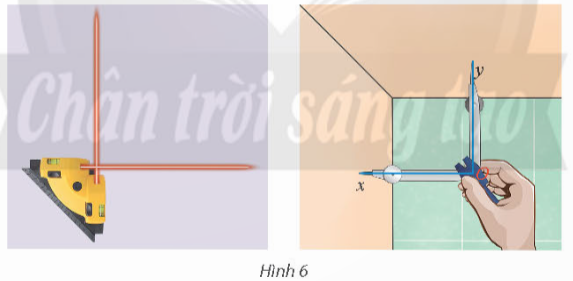
Đáp án chuẩn:

Bài 2: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d, điểm M không thuộc (P) và (Q). Gọi H và K lần lượt là hình chiếu vuông góc của M lên (P) và (Q). Gọi O là giao điểm của d và (MHK) (Hình 8)

a) Giả sử (P) ⊥ (Q), hãy cho biết tứ giác MHOK là hình gì? Tìm trong (P) đường thẳng vuông góc với (Q)

b) Giả sử (P) chứa đường thẳng a với a ⊥ (Q), hãy cho biết tứ giác MHOK là hình gì? Tính góc giữa (P) và (Q)

Đáp án chuẩn:

a) MHOK là hình chữ nhật.

Trong (P) có

b) MHOK là hình chữ nhật; Góc giữa (P) và (Q) là

Bài 3: Cho hình chóp S.ABCD có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:

a) (SAC)⊥(ABCD)

b) (SAC)⊥(SDB)

Đáp án chuẩn:

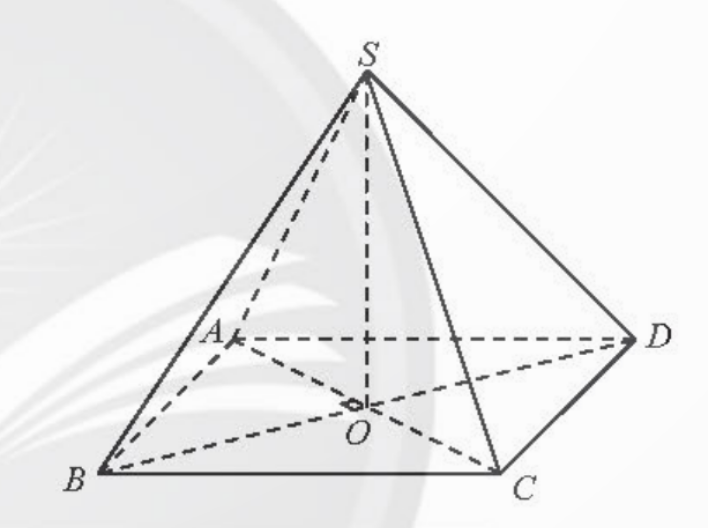
a) =>

b)  AC ⊥ (SBD) và (SAC) ⊥ (SBD)

Bài 4: Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.

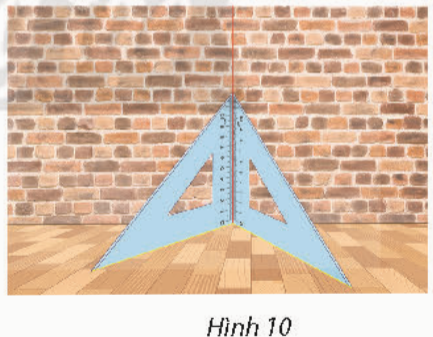
Đáp án chuẩn:

Đặt hai cái êke không trùng nhau sao cho mỗi eke có một cạnh nằm trên sàn và một cạnh trùng với đường thẳng d 

3. TÍNH CHẤT CƠ BẢN VỀ HAI MẶT PHẲNG VUÔNG GÓC

Bài 1: Cho đường thẳng a vuông góc với mặt phẳng (Q). Mặt phẳng (P) chứa a và cắt (Q) theo giao tuyến c. Trong (Q) vẽ đường thẳng b vuông góc với c. Hỏi

a) (P) có vuông góc với (Q) không?

b) Đường thẳng b vuông góc với (P) không? 

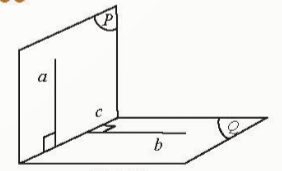
Đáp án chuẩn:

a)

b)

Bài 2: Cho hai mặt phẳng (P) và (Q) cùng vuông góc với mặt phẳng (R). Gọi a là giao tuyến của (P) và (Q). Lấy điểm M trong (R), vẽ hai đường thẳng MH và MK lần lượt vuông góc với (P) và (Q). Hỏi:

a) Hai đường thẳng MH và MK có nằm trong (R) không?

b) Đường thẳng a có vuông góc với (R) không?

Đáp án chuẩn:

a)

b)

Bài 3: Tứ diện ABCD có AB (BCD). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng (ACD) vẽ DK vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng:

a) (ACD) (ABE) và (ADC) (DFK)

b) OH (ADC)

Đáp án chuẩn:

a) =>.
  => .

b) Ta có là giao tuyến của và

 =>
Bài 4: Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.  

Đáp án chuẩn:

Đặt quyển sách sao cho đường thẳng gáy sách a vuông góc với bàn.

4. HÌNH LĂNG TRỤ ĐỨNG, HÌNH HỘP CHỮ NHẬT, HÌNH LẬP PHƯƠNG

Bài 1: a) Cho hình lăng trụ ABCDE.A'B'C'D'E' có cạnh bên AA' vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?

b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì về các mặt bên của hình lăng trụ này?

c) Một hình lăng trụ nếu có đáy là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?

d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18d) thì có bao nhiêu mặt là hình chữ nhật?

Đáp án chuẩn:

a) Mặt bên là các hình chữ nhật

b) Mặt bên là các hình chữ nhật bằng nhau

c) Bốn mặt bên đều là hình chữ nhật

d) Đều là hình chữ nhật.

Bài 2: Cho hình lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F' có cạnh bên bằng h và cạnh đáy bằng a. Tính A'C và A'D theo a và h

Đáp án chuẩn:

; ; ;

Bài 3: Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm và cạnh bên bằng 30 cm (Hình 20). Tính tổng diện tích các mặt bên của chiếc lồng đèn đó.

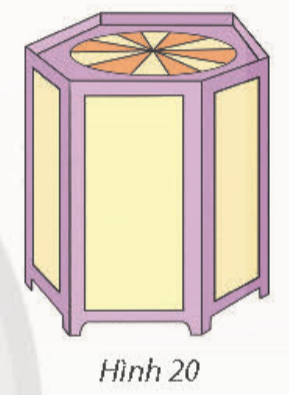
Đáp án chuẩn:

5. HÌNH CHÓP ĐỀU. HÌNH CHÓP CỤT 

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông với tâm O và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng SO có vuông góc với đáy không?

Đáp án chuẩn:

Bài 2: Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và AB = a; SA = 2a. Tính SO theo a

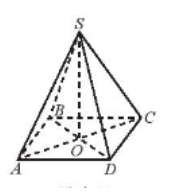
Đáp án chuẩn:

Bài 3: Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136 m và cạnh đáy dài khoảng 152 m. Tính độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp. 

Đáp án chuẩn:

Bài 4: Cho hình chóp đều S.A₁A₂A₃....A₆. Mặt phẳng (P) song song với mặt đáy và cắt các cạnh bên lần lượt tại A₁’; A₂’;A₃’;....;A₆’

a) Đa giác A₁’A₂’A₃’....A₆’ có phải lục giác đều không? Giải thích

b) Gọi O và O' lần lượt là tâm của hai lục giác A₁A₂A₃....A₆ và A₁’A₂’A₃’....A₆’. Đường thẳng OO' có vuông góc với mặt đáy không?

Đáp án chuẩn:

a) Đa giác là lục giác đều. 

b) OO’ vuông góc mặt đáy.

Bài 5: Cho hình chóp cụt tam giác đều ABC.A'B'C' có cạnh đáy lớn a, cạnh đáy nhỏ a/2 và cạnh bên 2a. Tính độ dài đường cao của hình chóp cụt đó.

Đáp án chuẩn:

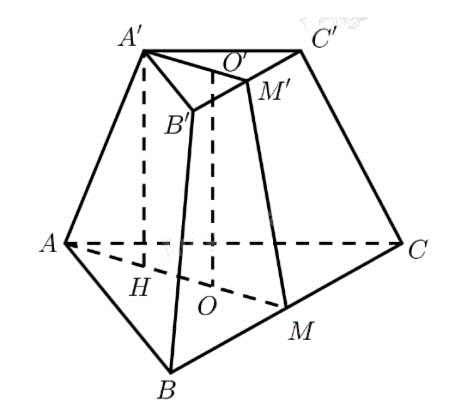
Bài 6: Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn. 

Đáp án chuẩn:

.

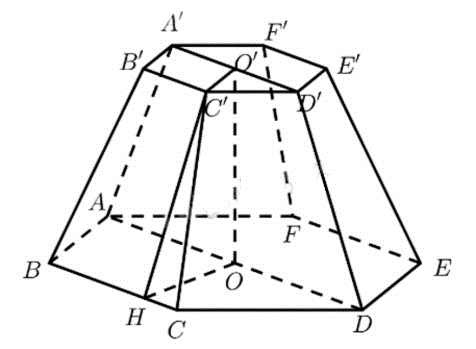
6. Bài tập

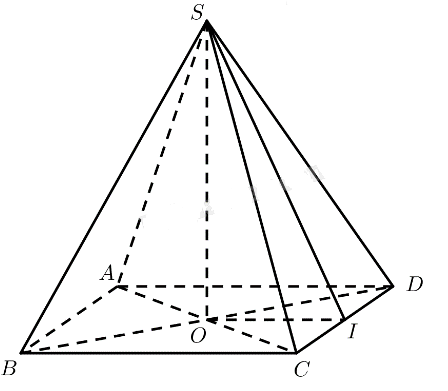
Bài 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với (ABC)

a) Chứng minh rằng (SBC) ⊥ (SAC)

b) Gọi I là trung điểm của SC. Chứng minh rằng (ABI) ⊥ (SBC)

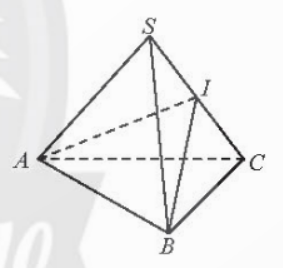
Đáp án chuẩn:

(SAC), suy ra .

b) . (1); . (2)

Từ (1) và (2) suy ra , suy ra .
Bài 2: Cho tam giác đều ABC cạnh a, I là trung điểm của BC, D là điểm đối xứng với A qua I. Vẽ đoạn thẳng SD có độ dài bằng và vuông góc với (ABC). Chứng minh rằng:

a) (SBC)⊥(SAD)

b) (SAB)⊥(SAC)

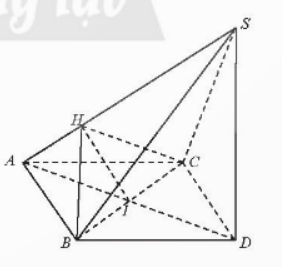
Đáp án chuẩn:

a) Ta có =>   => .

b) . (1); . (2)
Từ (1) và (2) => => .
Bài 3: Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông tại A và B, AA' = 2a, AD = 2a, AB = BC = a

a) Tính độ dài đoạn thẳng AC'

b) Tính tổng diện tích các mặt của hình lăng trụ.

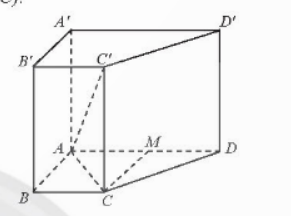
Đáp án chuẩn:

a) .
b) .

Bài 4: Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình thoi. Cho biết AB = BD =a, AC' = 2a

a) Tính độ dài đoạn thẳng AA'

b) Tính tổng diện tích các mặt của hình hộp

Đáp án chuẩn:

a) .
b) .

Bài 5: Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ và đường nối tâm hai đáy bằng a. Tính độ dài cạnh bên và đường cao của mỗi mặt bên

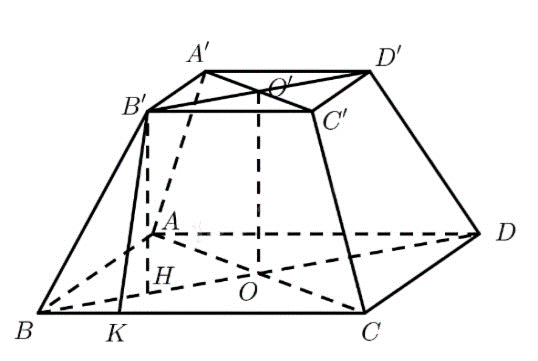
Đáp án chuẩn:

độ dài cạnh bên là độ dài đường cao mỗi mặt bên là .

Bài 6: Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp. 

Đáp án chuẩn:

độ dài cạnh bên bằng ;