Slide bài giảng Toán 11 chân trời Chương 8 Bài 2: Đường thẳng vuông góc với mặt phẳng

Tóm lược nội dung

BÀI 2. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG (3 TIẾT)

HOẠT ĐỘNG KHỞI ĐỘNG

- GV yêu cầu HS thảo luận và trả lời:

Trong thực tế, người thợ xây dựng thường sử dụng dây dọi để xác định các đường thẳng vuông góc với mặt nền. Vậy, thế nào là một đường thẳng vuông góc với mặt phẳng?

- GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.

NỘI DUNG BÀI HỌC GỒM

• Đường thẳng vuông góc với mặt phẳng
• Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng
• Phép chiếu vuông góc
• Luyện tập
• Vận dụng

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

1. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

Hoạt động 1: Tìm hiểu đường thẳng vuông góc với mặt phẳng

Khái quát định lí định lí quan trọng trong việc chỉ ra 1 đường thẳng vuông góc với mặt phẳng.

Nội dung ghi nhớ:

Định lí 1:

Nếu đường thẳng vuông góc với hai đường thẳng cắt nhau và cùng nằm trong mặt phẳng thì .

Định lí 2:

Có duy nhất một mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước.

Có duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.

2. LIÊN HỆ GIỮA TÍNH SONG SONG VÀ TÍNH VUÔNG GÓC CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

Hoạt động 2: Tìm hiểu mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng

Nêu một số định lí về mối liên hệ giữa tính song song và vuông góc của đường thẳng và mặt phẳng.

Nội dung ghi nhớ:

Định lí 3

a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia. 

b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Định lí 4

a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Định lí 5

a) Cho đường thẳng song song với mặt phẳng . Đường thẳng nào vuông góc với thì cũng vuông góc với . 

b) Nếu đường thẳng và mặt phẳng (không chứa ) cùng vuông góc với một đường thẳng thì chúng song song với nhau.

3. PHÉP CHIẾU VUÔNG GÓC

Hoạt động 3: Tìm hiểu phép chiếu vuông góc

Nêu khái niệm phép chiếu vuông góc.

Nêu định lí ba đường thẳng vuông góc

Nội dung ghi nhớ:

Định nghĩa

Cho mặt phẳng và đường thẳng vuông góc với . Phép chiếu song song theo phương của lên mặt phẳng được gọi là phép chiếu vuông góc lên .

*) Định lí ba đường vuông góc

Định lí 6

Cho đường thẳng nằm trong mặt phẳng và là đường thẳng không nằm trong và không vuông góc với . Gọi là hình chiếu vuông góc của trên . Khi đó vuông góc với khi và chỉ khi vuông góc với .

HOẠT ĐỘNG LUYỆN TẬP

Câu 1: AA' vuông góc với mặt phẳng:

A. (CDD'C')

B. (BCD)

C. (BCC'B')

D. (A'BD)

Câu 2: AC vuông góc với mặt phẳng:

A. (CDD'C')

B. (A'B'C'D')

C. (BDD'B')

D. (A'BD)

Câu 3: Hình chiếu vuông góc của A lên mặt phẳng (A'BD) là:

A. trung điểm của BD

B. trung điểm của A'B

C. trung điểm của A'D

D. tâm O của tam giác BDA'

Đề bài dùng cho câu 24, 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD)

Câu 4: Tam giác SBC là:

A. Tam giác thường

B. Tam giác cân

C. Tam giác đều

D. Tam giác vuông

Câu 5: Tam giác SOD là: 

A. Tam giác thường

B. Tam giác cân

C. Tam giác đều

D. Tam giác vuông

Nội dung ghi nhớ:

Câu 1: B

Câu 2: C

Câu 3: D

Câu 4: D

Câu 5: D

HOẠT ĐỘNG VẬN DỤNG

Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:

Câu 1: Cho hình chóp S.ABC có SA = SB = SC = a, = 90°, = 60° và = 120°. Gọi I là trung điểm cạnh AC. Chứng minh SI ⊥ (ABC) .

Câu 2: Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m

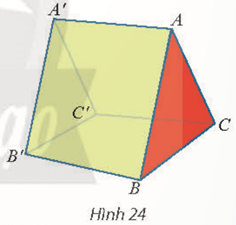
a) Tính góc giữa đường thẳng AA′ và BC; A ′B′ và AC.

b) Tính diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB ′CC′ )