Slide bài giảng Toán 11 chân trời Chương 3 Bài 3: Hàm số liên tục
Slide điện tử Bài 3: Hàm số liên tục. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 11 Chân trời sáng tạo sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3. HÀM SỐ LIÊN TỤC
1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Khám phá 1 (Trang 80):
Cho hàm số 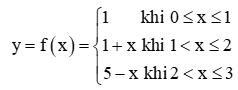 có đồ thị như Hình 1.
có đồ thị như Hình 1.
Tại mỗi điểm x0 = 1 và x0 = 2, có tồn tại giới hạn ![]() không? Nếu có, giới hạn đó có bằng f(x0) không?
không? Nếu có, giới hạn đó có bằng f(x0) không?
Trả lời rút gọn:
![]()
![]() .
.
Suy ra không tồn tại giới hạn![]() .
.![]()
![]() .
.
Suy ra tồn tại giới hạn ![]() .
.
Mặt khác, ![]() nên
nên ![]() .
.
Thực hành 1 (Trang 81):
Xét tính liên tục của hàm số:
a) f(x) = 1 – x2 tại điểm x0 = 3;
b) 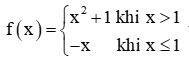 tại điểm x0 = 1.
tại điểm x0 = 1.
Trả lời rút gọn:
a) ![]() .
.
Vậy hàm số liên tục tại ![]() .
.
b) ![]()
![]() .
.
Suy ra không tồn tại giới hạn ![]() .
.
Do đó, hàm số không liên tục tại ![]() .
.
2. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG, TRÊN MỘT ĐOẠN
Khám phá 2 (Trang 81):
Cho hàm số 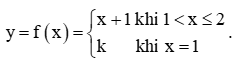 .
.
a) Xét tính liên tục của hàm số tại mỗi điểm x0 ∈ (1; 2).
b) Tìm ![]() và so sánh giá trị này với f(2).
và so sánh giá trị này với f(2).
c) Với giá trị nào của k thì ![]()
Trả lời rút gọn:
a) Với mọi ![]() , ta có
, ta có
![]() .
.
Vậy hàm số liên tục tại mọi điểm ![]() .
.
b) ![]() .
.
c) ![]() .
.
Vậy để ![]() , ta phải có
, ta phải có ![]() .
.
Thực hành 2 (Trang 82):
Xét tính liên tục của hàm số:
y = ![]()
Trả lời rút gọn:
Với mọi ![]() , ta có:
, ta có:
![]()
![]()
Do đó, hàm số liên tục tại mọi điểm ![]() .
.
Ta lại có:
![]()
![]()
Tương tự, ![]() .
.
Từ đó, hàm số liên tục trên [1:2].
Vận dụng 1 (Trang 82):
Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức sau:
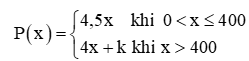 (k là một hằng số).
(k là một hằng số).
a) Với k = 0, xét tính liên tục của hàm số P(x) trên (0; +∞).
b) Với giá trị nào của k thì hàm số P(x) liên tục trên (0; +∞)?
Trả lời rút gọn:
a) Với ![]() tại mọi
tại mọi ![]() .
.
![]()
![]()
Do ![]() , nên
, nên ![]() không liên tục tại
không liên tục tại ![]() .
.
b) Ta cần tìm ![]() để hàm số liên tục tại
để hàm số liên tục tại ![]() .
.
![]()
![]()
Để ![]() liên tục tại
liên tục tại ![]() , ta phải có
, ta phải có ![]() suy ra
suy ra ![]() .
.
3. TÍNH LIÊN TỤC CỦA HÀM SỐ SƠ CẤP
Khám phá 3 (Trang 82):
Cho hai hàm số ![]()
a) Tìm tập xác định của mỗi hàm số đã cho.
b) Mỗi hàm số liên tục trên những khoảng nào? Giải thích.
Trả lời rút gọn:
a) Hàm số ![]() có tập xác định là
có tập xác định là ![]() ;
;
Hàm số ![]() có tập xác định là
có tập xác định là ![]() .
.
b)
+) Với ![]() , ta có
, ta có
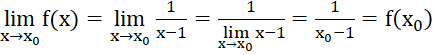 .
.
Vậy hàm số liên tục tại mọi điểm ![]() .
.
Suy ra hàm số liên tục trên các khoảng ![]() và
và ![]() .
.
+) Tương tự, chỉ ra được hàm số ![]() liên tục trên khoảng
liên tục trên khoảng ![]() .
.
Vì với ![]() , ta có
, ta có
![]()
Và ![]()
Thực hành 3 (Trang 83):
Xét tính liên tục của hàm số ![]()
Trả lời rút gọn:
Hàm số ![]() là hàm số căn thức, có tập xác định
là hàm số căn thức, có tập xác định ![]() .
.
Suy ra hàm số liên tục trên các khoảng ![]() và
và ![]() .
.
Thực hành 4 (Trang 83):
Cho hàm số f(x) = 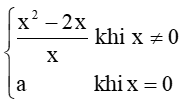 . Tìm a để hàm số y = f(x) liên tục trên ℝ.
. Tìm a để hàm số y = f(x) liên tục trên ℝ.
Trả lời rút gọn:
Do hàm số ![]() là hàm phân thức xác định khi
là hàm phân thức xác định khi ![]() nên
nên ![]() liên tục tại mọi điểm
liên tục tại mọi điểm ![]() .
.
Ta có ![]() . Từ đó, giá trị cần tìm là
. Từ đó, giá trị cần tìm là ![]() .
.
Vận dụng 2 (Trang 83):
Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:
T(x) = 
Xét tính liên tục của hàm số T(x).
Trả lời rút gọn:
+) Hàm số liên tục trên các khoảng ![]() và
và ![]() .
.
+) Xét hàm số liên tục tại x = 0,7.![]() ;
;
![]()
![]()
Ta thấy ![]() .
.
Do đó, hàm số liên tục tại ![]() .
.
+) Xét hàm số liên tục tại x = 20
![]()
![]()
![]()
![]()
Ta thấy ![]() .
.
Do đó, hàm số liên tục tại ![]() .
.
Vậy hàm số liên tục trên ![]() .
.
4. TỔNG, HIỆU, TÍCH, THƯƠNG CỦA HÀM SỐ LIÊN TỤC
Khám phá 4 (Trang 83):
Cho hai hàm số y = f(x) = 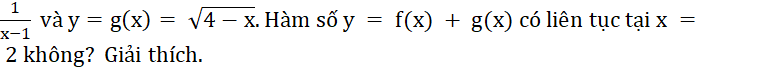
Trả lời rút gọn:
![]()
và ![]()
![]() .
.
Suy ra hàm số ![]() liên tục tại điểm
liên tục tại điểm ![]() .
.
Thực hành 5 (Trang 84):
Xét tính liên tục của hàm số:
a) ![]() +
+ ![]()
b) ![]()
Trả lời rút gọn:
a) Hàm số xác định trên ![]() . Do các hàm số
. Do các hàm số ![]() và
và ![]() liên tục trên
liên tục trên ![]() nên hàm số đã cho liên tục trên
nên hàm số đã cho liên tục trên ![]() .
.
b) Tập xác định: ![]() . Hàm số
. Hàm số ![]() liên tục tại mọi điểm
liên tục tại mọi điểm ![]() và hàm số
và hàm số ![]() liên tục trên
liên tục trên ![]() nên hàm số đã cho liên ṭ̣c tại mọi điểm
nên hàm số đã cho liên ṭ̣c tại mọi điểm ![]() (hay liên tụ̣c trên các khoảng
(hay liên tụ̣c trên các khoảng ![]() và
và ![]() .
.
Vận dụng 3 (Trang 84):
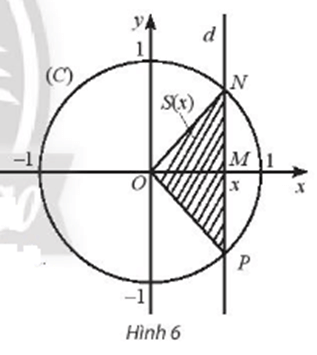
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Một đường thẳng d thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm M có hoành độ x (– 1 < x < 1) và cắt đường tròn (C) tại các điểm N và P (xem Hình 6).
a) Viết biểu thức S(x) biểu thị diện tích của tam giác ONP.
b) Hàm số y = S(x) có liên tục trên (– 1; 1) không? Giải thích.
c) Tìm các giới hạn ![]() .
.
Trả lời rút gọn:
a) ![]() với
với ![]() .
.
b) Hàm số liên tục trên (-1;1)
Vì hàm số ![]() và
và ![]() đều liên tục trên (-1;1)
đều liên tục trên (-1;1)
c) ![]() .
.
5. BÀI TẬP CUỐI SGK
Bài 1 (Trang 84):
Xét tính liên tục của hàm số sau:
a) f(x) = 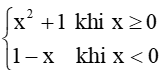 tại điểm x = 0;
tại điểm x = 0;
b) f(x) = 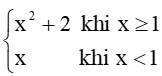 tại điểm x = 1.
tại điểm x = 1.
Trả lời rút gọn:
a)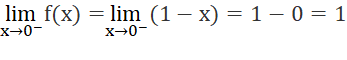
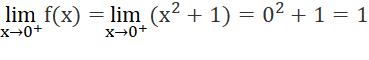
Suy ra: 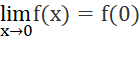
Vậy hàm số y = f(x) liên tục tại x = 0
b) 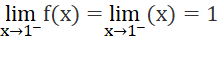
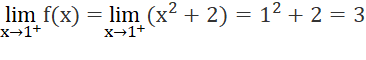
Suy ra không tồn tại 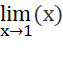
Vây hàm số không liên tục tại 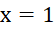 .
.
Bài 2 (Trang 84):
Cho hàm số f(x) = 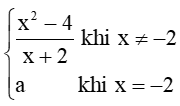 . Tìm a để hàm số f(x) liên tục trên ℝ.
. Tìm a để hàm số f(x) liên tục trên ℝ.
Trả lời rút gọn:
Hàm số liên tục tại mọi điểm ![]() .
.![]() .
.
Để hàm số liên tục tại ![]() , ta phải có
, ta phải có ![]() hay
hay ![]() .
.
Bài 3 (Trang 85):
Xét tính liên tục của hàm số sau:
a) f(x) = ![]()
b) ![]()
c) h(x) = cosx + tanx.
Trả lời rút gọn:
a) Hàm số liên tục tại trên các khoảng ![]() và
và ![]() .
.
b) Hàm số liên tục trên đoạn ![]() .
.
c) Hàm số liên tục tại mọi điểm ![]() với
với ![]() .
.
Bài 4 (Trang 85):
Cho hàm số f(x) = 2x – sinx, g(x) = ![]()
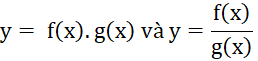
Trả lời rút gọn:
Hàm số ![]() liên tục trên
liên tục trên ![]() . Hàm số
. Hàm số ![]() liên tục trên
liên tục trên ![]() .
.
Bài 5 (Trang 85):
Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:
C(x) = 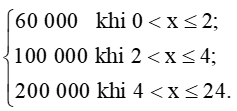
Xét tính liên tục của hàm số C(x).
Trả lời rút gọn:
+ Ta có :
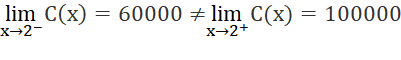
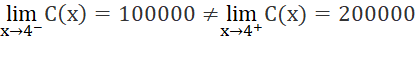
Hàm số gián đoạn tại các điểm ![]() và liên tục tại các điểm còn lại của khoảng
và liên tục tại các điểm còn lại của khoảng ![]()
Bài 6 (Trang 85):
Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r) = 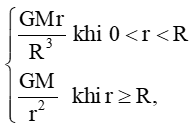 trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?
Trả lời rút gọn:
Hàm số liên tục trên các khoảng ![]() và
và ![]() .
.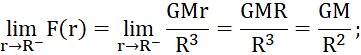
![]() .
.
Vậy ![]() , nên hàm số liên tục tại
, nên hàm số liên tục tại ![]() .
.
Do đó hàm số liên tục trên ![]() .
.
