Slide bài giảng Toán 11 chân trời Chương 2 Bài 2: Cấp số cộng

Tóm lược nội dung

BÀI 2. CẤP SỐ CỘNG

1. CẤP SỐ CỘNG

Khám phá 1 (Trang 52):

Tìm điểm giống nhau của các dãy số sau:

a) 2; 5; 8; 11; 14 (xem Hình 1).

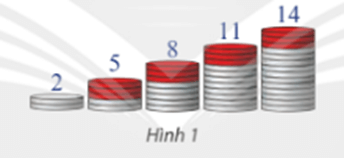
b) 2; 4; 6; 8.

c) 5; 10; 15; 20; 25.

d) – 5; – 2; 1; 4; 7; 10.

Trả lời rút gọn:

Các dãy số trên có điểm giống nhau:

Trong cùng một dãy số, số liền sau bằng tổng của số liền trước với một số không đổi.

Thực hành 1 (Trang 53):

Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.

a) 3; 7; 11; 15; 19; 23.

b) Dãy số (u_n) với u_n = 9n – 9.

c) Dãy số (v_n) với v_n = an + b, trong đó a và b là các hằng số.

Trả lời rút gọn:

a) Dãy số 3; 7; 11; 15; 19; 23 là cấp số cộng vì kể từ số hạng hứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 4.

b) Ta có: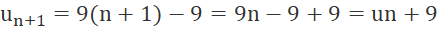

Vậy dãy số 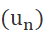là cấp số cộng có công sai d = 9

c) Ta có: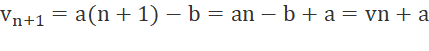

Vậy dãy số  là cấp số cộng có công sai d = a.

Thực hành 2 (Trang 53):

Số đo ba góc của một tam giác vuông lập thành một cấp số cộng. Tìm số đo ba góc đó.

Trả lời rút gọn:

3 góc của tam giác lập thành cấp số cộng, gọi 3 góc đó là: 

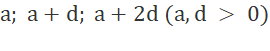
Ta có: 

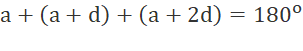
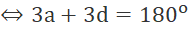
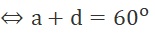(1)

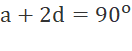Do tam giác đó là tam giác vuông nên có 1 góc bằng . Suy ra (2)

Từ (1) và (2), ta tính được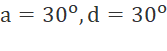

Vậy số đo 3 góc là

Vận dụng 1 (Trang 53):

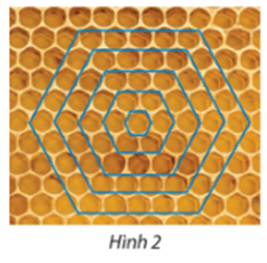
Mặt cắt của một tổ on có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quang vòng 2, cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.

Trả lời rút gọn:

Số ô trên các vòng là: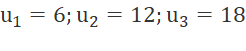

Ta thấy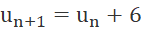

Vậy các ô trên vòng theo thứ tự tạo thành cấp số cộng có công sai là 6.

2. SỐ HẠNG TỔNG QUÁT CỦA CẤP SỐ CỘNG

Khám phá 2 (Trang 54):

Cho cấp số cộng (u_n). Hãy cho biết các hiệu số sau đây gấp bao nhiêu lần công sai d của (u_n) : u₂ – u₁; u₃ – u₁; u₄ – u₁; ...; u_n – u₁.

Trả lời rút gọn:

.....

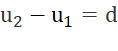
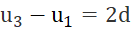
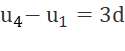
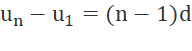
Thực hành 3 (Trang 54):

Tìm số hạng tổng quát của các cấp số cộng sau:

a) Cấp số cộng (a_n) có a₁ = 5 và d = – 5;

b) Cấp số cộng (b_n) có b₁ = 2 và b₁₀ = 20.

Trả lời rút gọn:

a)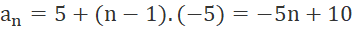

b)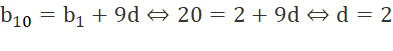

Suy ra số hạng tổng quát

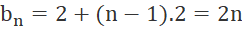
Vận dụng 2 (Trang 54):

Tìm số hạng tổng quát của cấp số cộng (c_n) có c₄ = 80 và c₆ = 40.

Trả lời rút gọn:

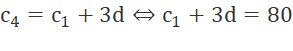
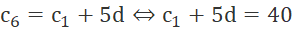
Suy ra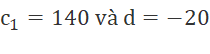

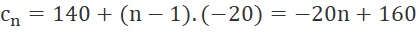
Vậy số hạng tổng quát của cấp số cộng là

3. TỔNG CỦA N SỐ HẠNG ĐẦU TIÊN CỦA CẤP SỐ CỘNG

Khám phá 3 (Trang 54):

Cho cấp số cộng (u_n) có công sai d.

a) Tính các tổng u_n + u₁; u₂ + u_n-1; u₃ + u_n-2; ...; u_k + u_n-k+1 theo u₁, n và d.

b) Chứng tỏ rằng 2(u₁ + u₂ + u₃ + ... + u_n) = n(u₁ + u_n).

Trả lời rút gọn:

a)

….

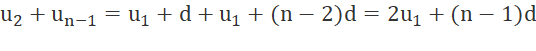
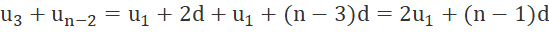
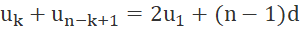
b) Theo a ta có

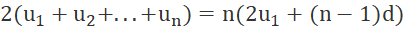
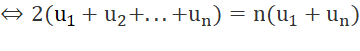
Thực hành 4 (Trang 55):

a) Tính tổng 50 số tự nhiên chẵn đầu tiên.

b) Cho cấp số cộng (u_n) có u₃ + u₂₈ = 100. Tính tổng 30 số hạng đầu tiên của cấp số cộng đó.

c) Cho cấp số cộng (v_n) có S₆ = 110. Tính S₂₀.

Trả lời rút gọn:

a) Tổng 50 số tự nhiên chẵn đầu tiên là:

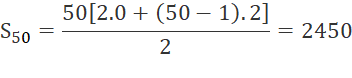
b)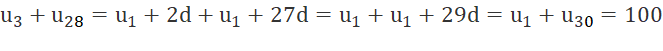

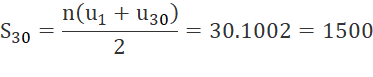
c)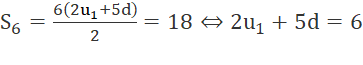

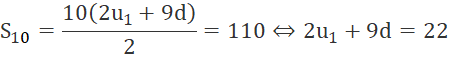
Suy ra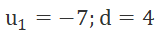

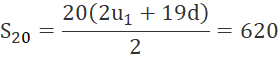
Vận dụng 3 (Trang 55):

Một rạp hát có 20 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 17 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 23 ghế, ... cứ thế tiếp tục cho đến hàng cuối cùng (Hình 4).

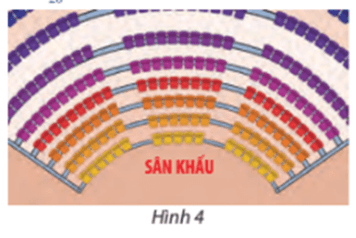
Trả lời rút gọn:

Ta có: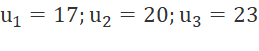

Suy r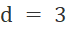a và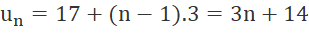

a)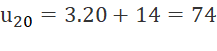

b)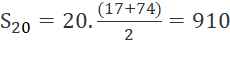

4. GIẢI BÀI TẬP CUỐI SGK

Bài 1 (Trang 56):

Chứng minh dãy số hữu hạn sau là cấp số cộng: 1; – 3; – 7; – 11; – 15.

Trả lời rút gọn:

Kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với nên dãy số là một cấp số cộng.

Bài 2 (Trang 56):

Cho (u_n­) là cấp số cộng với số hạng đầu u₁ = 4 và công sai d = – 10. Viết công thức số hạng tổng quát u_n.

Trả lời rút gọn:

Bài 3 (Trang 56):

Cho cấp số cộng (u_n­) có số hạng đầu u₁ = – 3 và công sai d = 2.

a) Tìm u₁₂;

b) Số 195 là số hạng thứ bao nhiêu của cấp số cộng đó?

Trả lời rút gọn:

a) ;
b) Ta có: . 

Vậy 195 là số hạng thứ 100 .

Bài 4 (Trang 56):

Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.

a) u_n = 3 – 4n;

b) u_n =

c) u_{n =}

d) u_n =

Trả lời rút gọn:

a) là cấp số cộng với số hạng đầu và công sai .
b) là cấp số cộng với số hạng đầu và công sai .
c) không phải là cấp số cộng vì có .
d) là cấp số cộng với số hạng đầu và công sai .

Bài 5 (Trang 56):

Tìm số hạng đầu và công sai của cấp số cộng (u_n), biết:

a) ;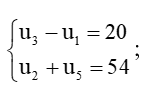

b) ;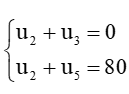

c) .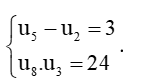

Trả lời rút gọn:

a)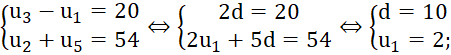
b)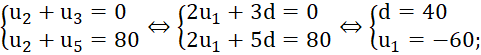
c)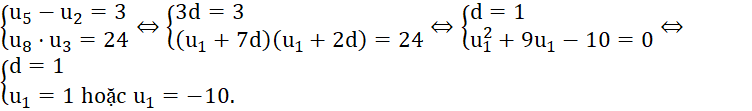

Bài 6 (Trang 56):

Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm, 41 cm, ..., 31 cm.

a) Cái thang đó có bao nhiêu bậc?

b) Tính chiều dài thanh gỗ mà người đó cần mua, giả sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể.

Trả lời rút gọn:

a) Chiều dài các thanh ngang của cái thang (tính từ bậc dưới cùng) tạo thành một cấp số cộng có: . Suy ra .
Vậy cái thang có 8 bậc.
b) . Vậy người đó cần mua thanh gỗ có chiều dài .

Bài 7 (Trang 56):

Khi một vận động viên nhảy dù nhảy xa khỏi máy bay, giả sử quãng đường người ấy rơi tự do (tính theo feet) trong mỗi giây liên tiếp theo thứ tự trước khi bung dủ lần lượt là: 16; 48; 80; 112; 144; ... (các quãng đường này tạo thành cấp số cộng).

a) Tính công sai của cấp số cộng trên.

b) Tính tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên.

Trả lời rút gọn:

a) .
b) (feet).

Bài 8 (Trang 56):

Ở một loài thực vật lưỡng bội, tính trạng chiều cao cây do hai gene không alen là A và B cùng quy định kiểu tương tác cộng gộp. Trong kiểu gene nếu cứ thêm một alen trội A hay B thì chiều cao cây tăng thêm 5 cm. Khi trưởng thành, cây thấp nhất của loài này với kiểu gene aabb có chiều cao 100cm. Hỏi cây cao nhất với kiểu gene AABB có chiều cao bao nhiêu? 

Trả lời rút gọn:

Chiều cao của các cây có số alen trội từ 0 đến 4 tạo thành 5 số hạng liên tiếp của một cấp số cộng với và , suy ra .