Slide bài giảng Toán 11 chân trời Chương 3 Bài 1: Giới hạn của dãy số
Slide điện tử Chương 3 Bài 1: Giới hạn của dãy số. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Chân trời sáng tạo sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 1. GIỚI HẠN CỦA DÃY SỐ
1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
Khám phá 1 (Trang 64):
Cho dãy số (un) với un = ![]()
a) Tìm các giá trị còn thiếu trong bảng sau:
| n | 10 | 20 | 50 | 100 | 1 000 |
| |un| | 0,1 | 0,05 | 0,02 | ? | ? |
b) Với n như thế nào thì |un| bé hơn 0,01; 0,001?
c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm un đến điểm 0 khi n trở lên rất lớn?
Trả lời rút gọn:
![]() .
.
a)
| 10 | 20 | 50 | 100 | 1000 |
| 0,1 | 0,05 | 0,02 |
|
|
b) ![]() .
.
Ta có: ![]() khi
khi ![]()
![]() khi
khi ![]() .
.
c)

Khoảng cách từ ![]() đến 0 trở nên rất bé khi n trở nên rất lớn.
đến 0 trở nên rất bé khi n trở nên rất lớn.
Thực hành 1 (Trang 65):
Tìm các giới hạn sau:
a) ![]()
b) ![]()
Trả lời rút gọn:
a) ![]() vì
vì ![]() , với
, với ![]() nguyên dương bất kì.
nguyên dương bất kì.
b) ![]() vì
vì ![]() , với
, với ![]() là số thực thoả mãn
là số thực thoả mãn ![]() trong trường hợp này
trong trường hợp này ![]() .
.
Khám phá 2 (Trang 65):
Cho dãy số (un) với un = ![]()
a) Cho dãy số (vn) với vn = un – 2. Tìm giới hạn lim vn.
b) Biểu diễn các điểm u1, u2, u3, u4 trên trục số. Có nhận xét gì về vị trí của các điểm un khi n trở nên rất lớn?
Trả lời rút gọn:
a) ![]()
![]()
b) ![]()
![]()
![]()
![]()
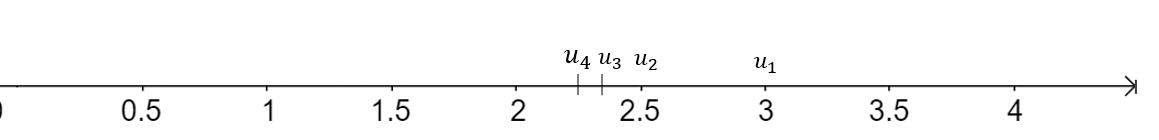
Nhận xét: Điểm ![]() càng dần đến điểm 2 khi n trở nên rất lớn.
càng dần đến điểm 2 khi n trở nên rất lớn.
Thực hành 2 (Trang 65):
Tìm các giới hạn sau:
a) ![]()
b) b) ![]()
Trả lời rút gọn:
a) ![]() , suy ra
, suy ra ![]() .
.
b) ![]() , suy ra
, suy ra ![]() .
.
