Slide bài giảng Toán 11 chân trời Bài tập cuối chương 4

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG IV

BÀI TẬP TỰ LUẬN

Bài 9 (Trang 128):

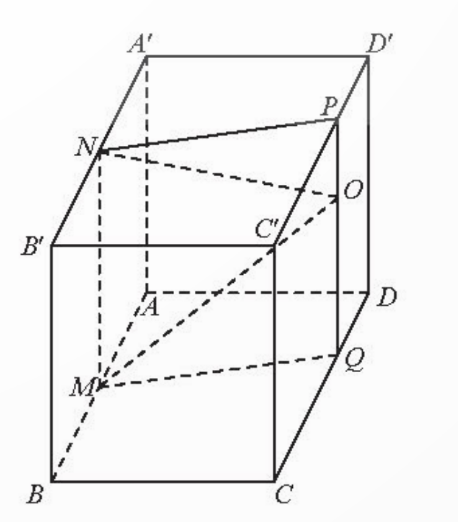
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của AB và A’B’ và O là một điểm thuộc miền trong của mặt bên CC’D’D. Tìm giao tuyến của mặt phẳng (OMN) với các mặt của hình hộp.

Trả lời rút gọn: 

Do các mặt đối diện của hình hộp song song nên (MNO) cắt các mặt đối diện của hình hộp theo từng cặp giao tuyến song song.

Qua vẽ đường thẳng và cắt tại , cắt tại .

Ta được các giao tuyến là .

Bài 10 (Trang 128):

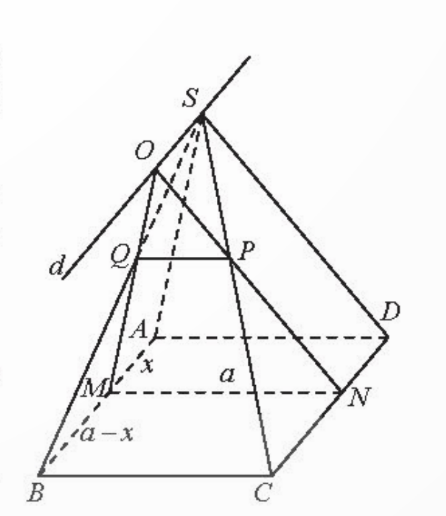
Cho hình chóp SABCD với ABCD là hình thoi cạnh a, tam giác SAD đều. M là điểm trên cạnh AB, (α) là mặt phẳng qua M và (α) // (SAD) cắt CD, SC, SD lần lượt tại N, P, Q.

a) Chứng minh rằng MNPQ là hình thang cân.

b) Đặt AM = x, tính diện tích MNPQ theo a và x.

Trả lời rút gọn: 

a) Ta có cắt hai mặt phẳng song song và theo hai giao tuyến song song và . Tương tự, ta cũng có .

Ta có , suy ra giao tuyến của và là thoả mãn . Gọi là giao tuyến của và ta có đi qua và .

Gọi là giao diểm của và , ta có thuộc .

Tứ giác là hình bình hành, suy ra . Tương tự ta có .

Tam giác là tam giác đều có cạnh bằng , suy ra là hình thang cân.

b) Ta có . Suy ra .

Ta có và là hai tam giác đều có cạnh là và , suy ra:

.

Bài 11 (Trang 128):

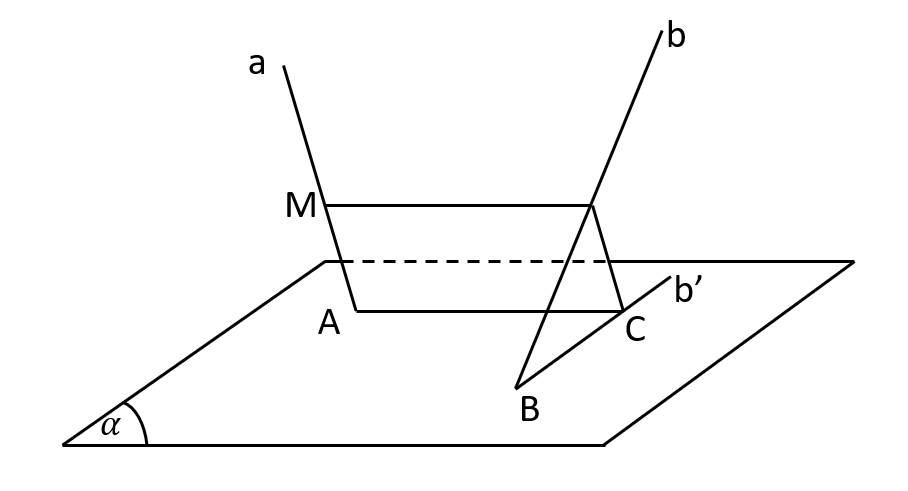
Cho mặt phẳng (α) và hai đường thẳng chéo nhau a, b cắt (α) tại A và B. Gọi d là đường thẳng thay đổi luôn luôn song song với (α) và cắt a tại M, cắt b tại N. Qua điểm N dựng đường thẳng song song với a cắt (α) tại điểm C.

a) Tứ giác MNCA là hình gì?

b) Chứng minh rằng điểm C luôn luôn chạy trên một đường thẳng cố định.

c) Xác định vị trí của đường thẳng d để độ dài MN nhỏ nhất.

Trả lời rút gọn: 

a) Ta có , suy ra giao tuyến của và là thoả mãn , suy ra là hình bình hành.

b) Gọi là giao tuyến của mặt phẳng và mặt phẳng (P) đi qua và song song với . Ta có cố định, suy ra cố định. Ta lại có , suy ra thuộc . Do là điểm chung của hai mặt phẳng và , suy ra di động trên .

c) Ta có , suy ra ngắn nhất khi và chỉ khi ngắn nhất. Vậy .

Bài 12 (Trang 128):

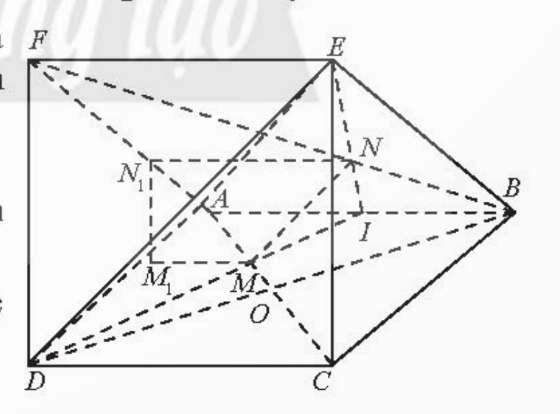
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng hoàn toàn khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC và BF sao cho MC = 2MA; NF = 2NB. Qua M, N kẻ các đường thẳng song song với AB, cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:

a) MN // DE;

b) M₁N₁ // (DEF);

c) (MNN₁M₁) // (DEF).

Trả lời rút gọn: 

a) Gọi là giao điểm của hai đường chéo của hình bình hành , ta có là đường trung tuyến của tam giác và . Suy ra là trọng tâm của tam giác . Tương tự, là trọng tâm của tam giác .

Gọi là trung điểm của thì lần lượ thuộc .

Xét tam giác có nên .

b) Ta có , suy ra ;

Ta có , suy ra ;

c) Ta có , suy ra .