Slide bài giảng Toán 11 chân trời Chương 3 Bài 2: Giới hạn của hàm số
Slide điện tử Bài 2: Giới hạn của hàm số. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 11 Chân trời sáng tạo sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 2. GIỚI HẠN CỦA HÀM SỐ
1. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
Khám phá 1 (Trang 71):
Xét hàm số y=f(x)=![]()
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
| x | 0 | 0,5 | 0,9 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,1 | 1,5 | 2 |
| f(x) | 2 | 3 | 3,8 | 3,98 | 3,998 | || | 4,002 | 4,02 | 4,2 | 5 | 6 |
Có nhận xét gì về giá trị của hàm số khi x càng gần đến 1?
b) Ở Hình 1, M là điểm trên đồ thị hàm số y = f(x); H và P lần lượt là hình chiếu của M trên trục hoành và trục tung. Khi điểm H thay đổi gần về điểm (1; 0) trên trục hoành thì điểm P thay đổi như thế nào?
Trả lời rút gọn:
a) Khi ![]() càng gần đến 1 thì giá trị của hàm số càng gần đến 4 .
càng gần đến 1 thì giá trị của hàm số càng gần đến 4 .
b) Điểm ![]() càng gần đến điểm
càng gần đến điểm ![]() trên trục tung khi điểm
trên trục tung khi điểm ![]() càng gần về điểm
càng gần về điểm ![]() trên trục hoành.
trên trục hoành.
Thực hành 1 (Trang 72):
Tìm các giới hạn sau:
![]()
b) ![]()
Trả lời rút gọn:
a) Giả sử ![]() là dãy số bất kì, thoả mãn
là dãy số bất kì, thoả mãn ![]() với mọi
với mọi ![]() và
và ![]() . Ta có
. Ta có
![]()
Vậy![]() .
.
b) Giả sử ![]() là dãy số bất kì, thoả mãn
là dãy số bất kì, thoả mãn ![]() với mọi
với mọi ![]() và
và ![]() khi
khi ![]() . Ta có
. Ta có
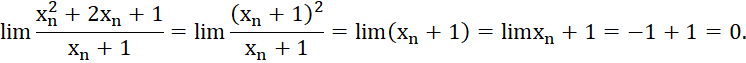
Vậy ![]() .
.
2. CÁC PHÉP TOÁN VỀ GIỚI HẠN HỮU HẠN CỦA HÀM SỐ
Khám phá 2 (Trang 72):
Cho hai hàm số y = f(x) = 2x và y = g(x) = ![]()
a) Giả sử (xn) là dãy số bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞. Tìm giới hạn lim[f(xn) + g(xn)].
b) Từ đó, tìm giới hạn ![]() và so sánh với
và so sánh với ![]()
Trả lời rút gọn:
a) Ta có ![]()
![]() .
.
b) Vì ![]()
nên ![]() .
.
Ta có: ![]()
![]()
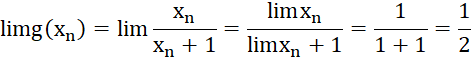
![]() .
.
Do đó ![]() .
.
Từ (1) và (2) suy ra
![]() .
.
Thực hành 2 (Trang 73):
Tìm các giới hạn sau:
a)![]()
b) ![]()
Trả lời rút gọn:
a)![]()
![]()
![]() .
.
b) ![]()
![]() .
.
3. GIỚI HẠN MỘT PHÍA
Khám phá 3 (Trang 73):
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị được cho bởi bảng sau:
| Khối lượng bưu kiện (100 gam) | Giá cước cận vùng (nghìn đồng) |
| đến 1 | 6 |
| trên 1 đến 2,5 | 7 |
| từ 2,5 đến 5 | 10 |
| ... | ... |
Nếu chỉ xét trên khoảng từ 0 đến 5 (tính theo 100 gam) thì hàm số giá cước (tính theo nghìn đồng) xác định như sau:
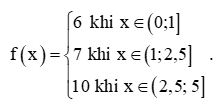
Đồ thị của hàm số như Hình 2.
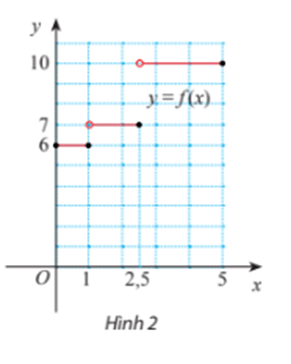
a) Giả sử (xn) là dãy số bất kì sao cho xn ∈ (1; 2,5) và lim xn = 1. Tìm lim f(xn).
b) Giả sử (x′n) là dãy số bất kì sao cho (x′n)∈(0;1) và limx′n=1. Tìm limf(x′n)
c) Nhận xét về kết quả ở a) và b).
Trả lời rút gọn:
a) Khi ![]() thì
thì ![]() nên
nên ![]() .
.
b) Khi ![]() thì
thì ![]() nên
nên ![]() .
.
c) Ta thấy, mặc dù ![]() nhưng
nhưng ![]() .
.
Thực hành 3 (Trang 75):
Cho hàm số 
Tìm các giới hạn ![]()
![]()
Trả lời rút gọn:
Cách 1: Sử dụng dãy số như định nghĩa.
Cách 2: (Sử dụng biểu thức xác định hàm số trên từng khoảng)
Với ![]() nên
nên
![]() .
.
Với ![]() nên
nên
![]() .
.
Do ![]() nên
nên ![]() .4. Giới hạn hữu hạn của hàm số tại vô cực
.4. Giới hạn hữu hạn của hàm số tại vô cực
4. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
Khám phá 4 (Trang 75):
Cho hàm số f(x)=![]() có đồ thị như Hình 3.
có đồ thị như Hình 3.
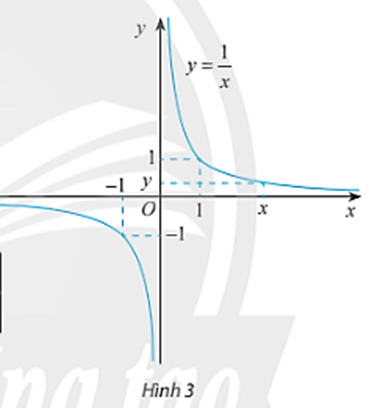
a) Tìm các giá trị còn thiếu trong bảng sau:
| x | 10 | 100 | 1 000 | 10 000 | 100 000 |
| y = f(x) | 0,1 | 0,01 | ? | ? | ? |
Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng lớn (dần tới +∞)?
b) Tìm các giá trị còn thiếu trong bảng sau:
| x | – 100 000 | – 10 000 | – 1 000 | – 100 | – 10 |
| y = f(x) | ? | ? | ? | –0,01 | –0,1 |
Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng bé (dần tới – ∞)?
Trả lời rút gọn:
a)
| x | 10 | 100 | 1 000 | 10 000 | 100 000 |
| y=f(x) | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 |
Giá trị của ![]() dần về 0 khi
dần về 0 khi ![]() dần tới
dần tới ![]() .
.
b)
| x | -100 000 | -10 000 | -1 000 | -100 | -10 |
| y=f(x) | -0,0001 | -0,00001 | -0,001 | -0,01 | -0,1 |
Giá trị của ![]() dần về 0 khi
dần về 0 khi ![]() dần tới
dần tới ![]() .
.
Thực hành 4 (Trang 76):
Tìm các giới hạn sau:
a) ![]()
b) ![]()
Trả lời rút gọn:
a) 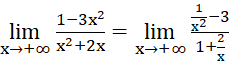
 ;
;
b) 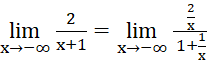
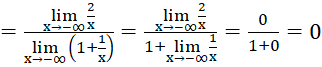 .
.
Vận dụng 1 (Trang 76):
Một cái hồ đang chứa 200m3 nước mặn với nồng độ muối 10kg/m3. Người ta ngọt hóa nước hồ bằng cách bơm nước ngọt vào hồ với tốc độ 2m3/phút.
a) Viết biểu thức C(t) biểu thị nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn ![]() và giải thích ý nghĩa.
và giải thích ý nghĩa.
Trả lời rút gọn:
a) Khối lượng muối có trong hồ là ![]() .
.
Sau ![]() phút, lượng nước trong hồ là
phút, lượng nước trong hồ là ![]() .
.
Nồng độ muối tại thời điểm ![]() phút kể từ khi bơm là
phút kể từ khi bơm là ![]() .
.
b)
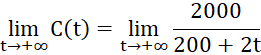
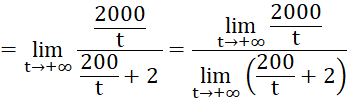
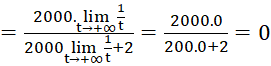 .
.
Điều này có nghĩa là khi ![]() càng lớn thì nồng độ muối càng dần về 0 , tức đến một lúc nào đó nồng độ muối trong hồ không còn đáng kể và nước trong hồ gần như là nước ngọt.
càng lớn thì nồng độ muối càng dần về 0 , tức đến một lúc nào đó nồng độ muối trong hồ không còn đáng kể và nước trong hồ gần như là nước ngọt.
5. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI MỘT ĐIỂM
Khám phá 5 (Trang 77):
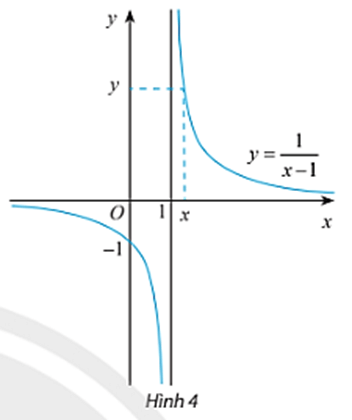
Cho hàm số f(x)=![]() có đồ thị như Hình 4.
có đồ thị như Hình 4.
a) Tìm các giá trị còn thiếu trong bảng sau:
| x | 1,1 | 1,01 | 1,001 | 1,0001 |
| y = f(x) | 10 | 100 | ? | ? |
Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:
| x | 0,9 | 0,99 | 0,999 | 0,9999 |
| y = f(x) | – 10 | – 100 | ? | ? |
Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên trái?
Trả lời rút gọn:
a)
x | 1,1 | 1,01 | 1,001 | 1,0001 |
y=f(x) | 10 | 100 | 1000 | 10 000 |
Giá trị của ![]() trở nên rất lớn khi
trở nên rất lớn khi ![]() dần tới 1 phía bên phải.
dần tới 1 phía bên phải.
b)
| x | 0,9 | 0,99 | 0,999 | 0,9999 |
| y = f(x) | -10 | -100 | -1000 | -10000 |
Giá trị của ![]() trở nên rất bé (giá trị của
trở nên rất bé (giá trị của ![]() trở nên rất lớn) khi
trở nên rất lớn) khi ![]() dần tới 1 phía bên trái.
dần tới 1 phía bên trái.
Thực hành 5 (Trang 78):
Tìm các giới hạn sau:
a) ![]()
b) ![]()
Trả lời rút gọn:
a) ![]() và
và ![]()
nên ![]() ;
;
b) ![]() và
và ![]()
nên ![]() .
.
Vận dụng 2 (Trang 78):
Xét tình huống ở hoạt động khởi động đầu bài học. Gọi x là hoành độ điểm H. Tính diện tích S(x) của hình chữ nhật OHMK theo x. Diện tích này thay đổi như thế nào khi x → 0+ và khi x → +∞.
Trả lời rút gọn:
Ta có ![]() .
.
![]() .
.
6. BÀI TẬP CUỐI SGK
Bài 1 (Trang 79):
Tìm các giới hạn sau:
a) ![]()
b) ![]()
c) ![]()
Trả lời rút gọn:
a) ![]() 22 ;
22 ;
b) ![]() ;
;
c) 
Bài 2 (Trang 79):
Cho hàm số  .
.
Tìm các giới hạn sau: ![]() (nếu có).
(nếu có).
Trả lời rút gọn:
![]() . Không tồn tại
. Không tồn tại ![]() .
.
Bài 3 (Trang 79):
Tìm các giới hạn sau:
a) ![]()
b) ![]()
c) 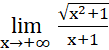
Trả lời rút gọn:
a) 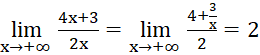 ;
;
b) 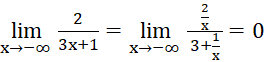
c) 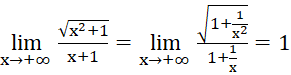
Bài 4 (Trang 79):
Tìm các giới hạn sau:
a) ![]()
b) ![]()
c) ![]()
Trả lời rút gọn:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
Bài 5 (Trang 79):
Trong hồ có chứa 6 000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là ![]() (gam/lít).
(gam/lít).
b) Nồng độ muối như thế nào nếu t → +∞.
Trả lời rút gọn:
a) ![]() (gam/lít).
(gam/lít).
b)  (gam/lít).
(gam/lít).
Bài 6 (Trang 79):
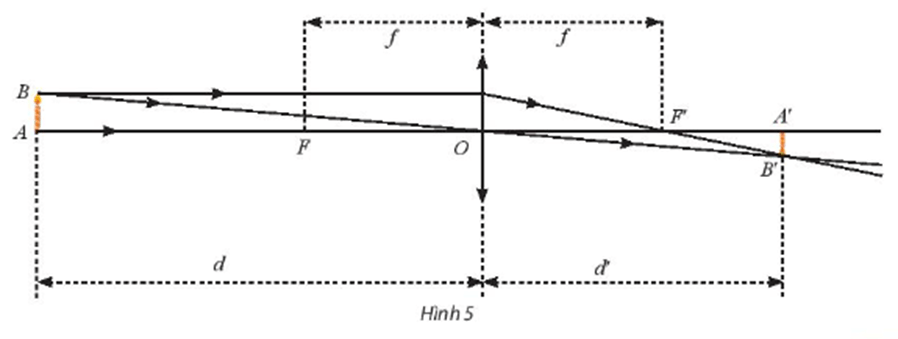
Một thấu kính hội tụ có tiêu cự là f > 0 không đổi. Gọi d và d’ lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Ta có công thức ![]()
Xét hàm số g(d)=![]() . Tìm các giới hạn sau đây và giải thích ý nghĩa.
. Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) ![]()
b) ![]()
Trả lời rút gọn:
a) ![]() .
.
Nghĩa là khi vật dần đến tiêu điểm vật ![]() từ phía xa kính đến gần kính hơn thì khoảng cách từ ảnh (thật) đến kính dần đến
từ phía xa kính đến gần kính hơn thì khoảng cách từ ảnh (thật) đến kính dần đến ![]() .
.
b)  .
.
Nghĩa là khi khoảng cách từ vật đến kính dần đến ![]() thì ảnh dần đến tiêu điểm ảnh
thì ảnh dần đến tiêu điểm ảnh ![]() .
.
