Slide bài giảng Toán 11 chân trời Bài tập cuối chương 7

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG VII (2 TIẾT)

HOẠT ĐỘNG KHỞI ĐỘNG

- GV yêu cầu HS trả lời và giải thích các câu hỏi TN 1 đến 5 (SGK -tr.51).

- GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.

- GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học: Bài tập cuối chương VII.

Đáp án: 1. B ; 2. A ; 3. D ; 4. C ; 5. D

NỘI DUNG BÀI HỌC GỒM

• Ôn tập các kiến thức đã học ở chương VII
• Luyện tập
• Vận dụng

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Hoạt động: Ôn tập các kiến thức đã học ở chương VII

Định nghĩa đạo hàm là gì?

Ý nghĩa vật lý của đạo hàm là gì?

Công thức viết phương trình tiếp tuyến là gì?

Số e là gì?

Bảng đạo hàm của hàm số sơ cấp và hàm hợp gồm những gì?

Quy tắc tính đạo hàm của tổng, hiệu, tích, thương được trình bày như thế nào?

Định nghĩa đạo hàm cấp hai là gì?

Ý nghĩa cơ học của đạo hàm cấp hai ra sao?

Nội dung ghi nhớ:

Định nghĩa đạo hàm: 

Cho hàm số xác định trên khoảng và .

Nếu tồn tại giới hạn hữu hạn 

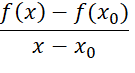
Thì giới hạn này được gọi là đạo hàm của hàm số f(x) tại , kí hiệu là hoặc .

Vậy: .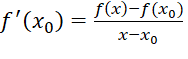

Ý nghĩa vật lí của đạo hàm

• Nếu hàm số 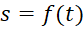biểu thị quãng đường di chuyển của vật theo thời gian 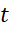thì 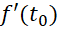biểu thị tốc độ tức thời của chuyển động tại thời điểm .
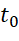• Nếu hàm số 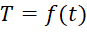biểu thị nhiệt độ 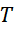theo thời gian 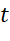thì 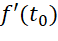biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm .

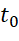Phương trình tiếp tuyến

Cho hàm số xác định trên khoảng và có đạo hàm tại . Gọi là đồ thị của hàm số đó.

Đạo hàm của hàm số tại điểm là hệ số góc của tiếp tuyến của tại điểm

Tiếp tuyến  có phương trình là:

Số e

Tổng quát, nếu một năm được chia thành kì hạn thì

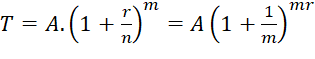(với .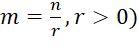

Khi kì hạn càng ngắn thì càng lớn, do đói càng lớn. Người ta chứng minh được rằng có giới hạn hữu hạn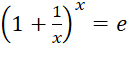

(với là số vô tỉ và

Khi kì hạn trở nên rất ngắn (m dần đến ) thì 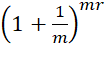dần đến , và do đó 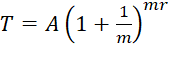dần đến .

Bảng đạo hàm của một số hàm sơ cấp và hàm hợp:

Đạo hàm của tổng, hiệu, tích thương

Cho hai hàm số có đạo hàm tại điểm thuộc tập xác định. Ta có:

• 
• 
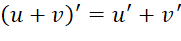
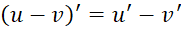
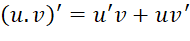• (1)
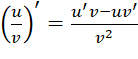• (với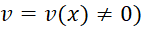  

Định nghĩa đạo hàm cấp hai: Cho hàm số có đạo hàm tại mọi .

Nếu hàm số có đạo hàm tại thì ta gọi đạo hàm của là đạo hàm cấp hai của hàm số tại , kí hiệu hoặc .

Ý nghĩa cơ học của đạo hàm cấp hai: Đạo hàm cấp hai là gia tốc tức thời tại thời điểm của vật chuyển động có phương trình .

HOẠT ĐỘNG LUYỆN TẬP

Câu 1: Cho hàm số g(x)=xf(x)+x, với f(x) là hàm số có đạo hàm trên R. Biết g'(3) = 2, f'(3) = -1. Giá trị của g(3) bằng:

A. -3

B. 3

C. 20

D. 15

Câu 2: Cho chuyển động thẳng xác định bởi phương trình  s(t)=t³+3t²−9t+27, trong đó t tính bằng giây (s) và s tính bằng mét (m). Gia tốc của chuyển động tại thời điểm vận tốc triệt tiêu là:

A. 0 m/s2

B. 6 m/s2

C. 24 m/s2

D. 12 m/s2

Câu 3: Một bình nuôi cấy vi sinh vật được giữ ở nhiệt độ 0 độ C. Tại thời điểm t = 0, người ta cung cấp nhiệt cho nó. Nhiệt độ của bình bắt đầu tăng lên và tại mỗi thời điểm t, nhiệt độ của nó được ước tính bởi hàm số 

f(t)=(t−1)³+1 (độ C). So sánh tốc độ tăng nhiệt độ của bình tại hai thời điểm t1= 0,5s và t2 = 1,25s.

A. Nhiệt độ tại thời điểm t1 tăng nhanh hơn tại thời điểm t2

B. Nhiệt độ tại thời điểm t1 và t2 tăng như nhau

C. Nhiệt độ tại thời điểm t2 tăng nhanh hơn tại thời điểm t2

D. Không đủ dữ liệu để kết luận 

Câu 4: Cho hàm số g(x)=xf(x)+x, với f(x) là hàm số có đạo hàm trên R. Biết g'(3) = 2, f'(3) = -1. Giá trị của g(3) bằng:

• A. -3
• B. 3
• C. 20
• D. 15

Câu 5: Tiếp tuyến của đồ thị hàm số 

y=2x³+3x² tại điểm M có tung độ bằng 5 là:

A. y = -12x - 7

B. y = 12x - 7

C. y = -12x + 17

D. y = 12x + 17

Nội dung ghi nhớ:

Câu 1: D

Câu 2: D

Câu 3: A

Câu 4: D

Câu 5: B

HOẠT ĐỘNG VẬN DỤNG

Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:

Bài 1: Một viên sỏi rơi từ độ cao 44,1 m thì quãng đường rơi được biểu diễn bởi công thức s(t) = 4,9t², trong đó t là thời gian tính bằng giây và s tính bằng mét. Tính:

a) Vận tốc của viên sỏi tại thời điểm t = 2 giây

b) Vận tốc của viên sỏi khi chạm đất

Bài 2: Một vật chuyển động trên đường thẳng được xác định bởi công thức s(t) = 2t³ + 4t + 1, trong đó t là thời gian tính bằng giây và s tính bằng mét. Tính vận tốc và gia tốc của vật khi t = 1 giây

Bài 3: Dân số P (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức P(t) = , trong đó t là thời gian được tính bằng năm. Tìm tốc độ tăng dân số tại thời điểm t = 12 năm

Bài 4: Hàm số S(r) = có thể được sử dụng để xác định sức cản S của dòng máu trong mạch máu có bán kính r (tính theo milimet) (theo Bách khoa toàn thư Y học "Harrison's internal medicine 21st edition"). Tìm tốc độ thay đổi của S theo r khi r = 0,8 milimet