Slide bài giảng Toán 11 chân trời Chương 1 Bài 3: Các công thức lượng giác

Tóm lược nội dung

BÀI 3. CÁC CÔNG THỨC LƯỢNG GIÁC

1. CÔNG THỨC CỘNG

Khám phá 1 (Trang 21):

 Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ sau đây:

x_M.x_N +y_M.y_{N ,}

Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.

Trả lời rút gọn:

(định nghĩa của tích vô hướng)

Vì và lần lượt là điểm biểu diễn của các góc lượng giác và trên đường tròn lượng giác, nên toạ độ của các điểm này là và .

Do đó

Vậy .

Suy ra .

Thực hành 1 (Trang 21):

Tính tan

Trả lời rút gọn:

;

2. CÔNG THỨC GÓC NHÂN ĐÔI

Khám phá 2 (Trang 21):

Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.

Trả lời rút gọn:

.

Mà .

Hoặc .

.

.

Thực hành 2 (Trang 22):

Tính và

Trả lời rút gọn:

Vì nên . Do đó .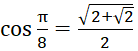

.

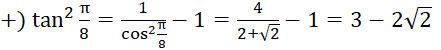Vì nên tan . 

Do đó .

3. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG

Khám phá 3 (Trang 22):

Từ công thức cộng, hãy tính tổng và hiệu của:

a)

b)

Trả lời rút gọn:

a)

b)

.

Thực hành 3 (Trang 22):

Tính giá trị của và 

Trả lời rút gọn:

.

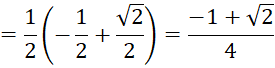
4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH

Khám phá 4 (Trang 22):

Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác a= và b= ta được các đẳng thức nào?

Trả lời rút gọn:

.

.

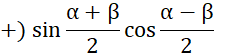
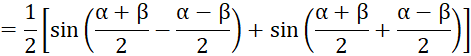
Thực hành 4 (Trang 23):

Tính

Trả lời rút gọn:

.

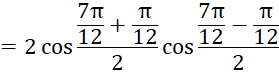
Vận dụng (Trang 23):

Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Trả lời rút gọn:

Đặt . Ta có .

Vì nên , suy ra .

Khoảng cách từ đến là .

5. GIẢI BÀI TẬP CUỐI SGK

Bài 1 (Trang 23):

Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:

a)

b)

Trả lời rút gọn:

a) ;

;

.

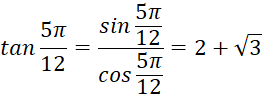
b)

;

.

Bài 2 (Trang 23):

Tính biết sin

Trả lời rút gọn:

Vì nên .

.

.

Bài 3 (Trang 24):

Tính các giá trị lượng giác của góc 2α, biết:

a)

b) .

Trả lời rút gọn:

a) Vì nên , suy ra

.

.

b) Ta có suy ra nên .

Do đó .

.

.

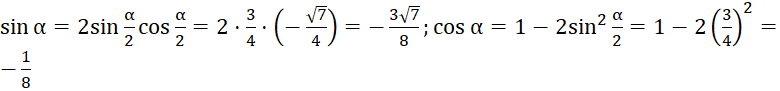Bài 4 (Trang 24):

Rút gọn các biểu thức sau:

a) ;

b)

Trả lời rút gọn:

a)

b) .

Bài 5 (Trang 24):

Tính các giá trị lượng giác của góc α, biết:

a)

b)

Trả lời rút gọn:

a) . Do đó .

Vì nên . Do đó .

Vì nên . Do đó .

.

b) Vì nên . Do đó .

.

Vì nên . Do đó .

Vì nên . Do đó .

.

Bài 6 (Trang 24):

Chứng minh rằng trong tam giác ABC, ta có:

.

Trả lời rút gọn:

Trong tam giác , ta có .

Do đó

Bài tập 7 trang 24 sgk toán 11 tập 1 CTST

Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn =30°. Tính tan , từ đó tính độ dài cạnh CD.

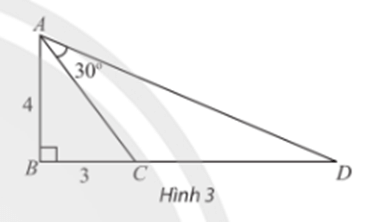
Trả lời rút gọn:

Đặt . Vì tam giác vuông tại nên tan .

Suy ra .

Ta có .

Vậy .

Bài 8 (Trang 24):

Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi α= và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8cm, viết công thức tính tọa độ x_M của điểm M trên trục Ox theo α.

b) Ban đầu α = 0. Sau 1 phút chuyển động, x_M = – 3cm. Xác định x_M sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.

Trả lời rút gọn:

a) Vì độ dài xem như không đổi và khi thì , nên ta xem như luôn bằng .

Do đó , hay toạ độ của trên trục bằng tọa độ của trên trục .

Suy ra .

b) Giả sử sau 1 phút chuyển động, quay được một góc thì sau 2 phút chuyển động, quay được một góc .

Ta có sau 1 phút chuyển động thì . Suy ra .

Do đó sau 2 phút chuyển động thì .

Bài 9 (Trang 24):

Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là và số đo góc (OA, OM) là α.

a) Tính sinα và cosα.

b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Trả lời rút gọn:

a) Trong hệ truc toạ đô như hình, ta có điểm nằm ở góc phần tư thứ IV.

Do đó .

b)

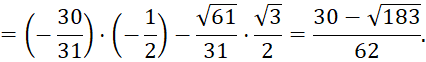
Khoảng cách từ đến mặt đất là .

.

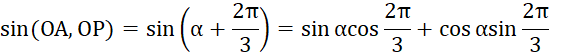
Khoảng cách từ đến mặt đất là .