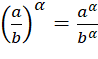Slide bài giảng Toán 11 chân trời Bài tập cuối chương 6

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG VI (2 TIẾT)

HOẠT ĐỘNG KHỞI ĐỘNG

- GV yêu cầu HS trả lời và giải thích các câu hỏi TN 1 đến 10 (SGK -tr.34).

- GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.

- GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học: Bài tập cuối chương VI.

Đáp án: 1. D, 2. A, 3. B, 4. B, 5. C, 6. D, 7. A, 8. A, 9. C, 10. D

NỘI DUNG BÀI HỌC GỒM

• Ôn tập các kiến thức đã học ở chương VI
• Luyện tập
• Vận dụng

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

1. ÔN TẬP CÁC KIẾN THỨC ĐÃ HỌC Ở CHƯƠNG VI

Hoạt động: Ôn tập các kiến thức đã học ở chương VI

Khi nào một số thực a được gọi là căn bậc n (với n là số nguyên dương, n ≥ 2) của b?

Các tính chất của phép tính lũy thừa là gì?

Các tính chất của phép tính lôgarit là gì?

Tập xác định của hàm số mũ y = ax (với a > 0 và a ≠ 1) và hàm số y = loga(x) (với a > 0 và a ≠ 1) là gì?

Làm thế nào để tìm nghiệm của phương trình mũ ax = b (với a > 0 và a ≠ 1)?

Cách giải bất phương trình mũ ax > b và bất phương trình lôgarit cơ bản log_a(x) > b (với a > 0 và a ≠ 1) như thế nào?

Nội dung ghi nhớ:

+) Cho số nguyên dương và số thực bất kì. Nếu có số thực sao cho

Thì được gọi là căn bậc của b.

+) Cho là những số thực dương; là những số thực bất kì. Khi đó:

+) Cho các số thực dương với , ta có:

+ Tập xác định hàm số là

+ Hàm số có tập xác định:

+ Cho phương trình .

Nếu thì phương trình luôn có nghiệm duy nhất . 

*)  Nghiệm của bất phương trình

 (1)

- Nếu thì mọi đều là nghiệm của (3).

- Nếu thì:

+ Với , nghiệm của (1) là ;

+ Với , nghiệm của (1) là .

*) Nghiệm bất phương trình:

Điều kiện xác định của bất phương trình là .

- Với , nghiệm của (2) là .

- Với , nghiệm của (2) là .

HOẠT ĐỘNG LUYỆN TẬP

HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn thành các bài tập GV yêu cầu.

Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.

Câu 1: Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4%/tháng. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được cộng vào vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau 6 tháng, người đó nhận được số tiền (cả vốn ban đầu và lãi) gần nhất với số nào sau đây (giả sử trong khoảng thời gian này người đó không rút tiền ra và lãi suất không thay đổi)?

A. 102 160 000 đồng

B. 102 017 000 đồng

C. 102 424 000 đồng

D. 102 423 000 đồng

Câu 2: Tìm các giá trị thực của tham số m để hàm số ln(x2−2x+m+1) có tập xác định là R

A. 0 < m < 3

B. m < -1 hoặc m > 0

C. m > 0

D. m = 0

Câu 3: Cho hai hàm số 

y = f(x) = logax và y=g(x)=a^X (0<a≠1). Xét các mệnh đề sau:

1. Đồ thị của hai hàm số f(x) và g(x) luôn cắt nhau tại một điểm

2. Hàm số f(x) + g(x) đồng biến khi a > 1, nghịch biến khi 0 < a < 1

3. Đồ thị hàm số f(x) nhận trục Oy làm tiệm cận

4. Chỉ có đồ thị hàm số f(x) có tiệm cận

Có bao nhiêu mệnh đề đúng?

A. 1

B. 2

C. 3

D. 4

Câu 4: Hình vẽ dưới đây biểu diễn đồ thị của hàm số nào?

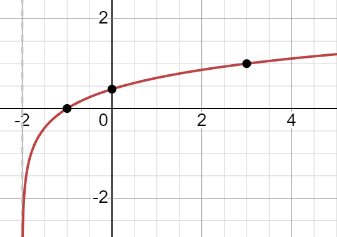
A. y=log5(x+2)

B. y=log5(x−2)

C.y=log2(x+5)

D.y=log2(x−5)

Câu 5: Tìm các giá trị thực của tham số m để hàm số ln(x²−2x+m+1) có tập xác định là R

A. 0 < m < 3

B. m < -1 hoặc m > 0

C. m > 0

D. m = 0

Nội dung ghi nhớ:

Câu 1: C

Câu 2: C

Câu 3: D

Câu 4: A

Câu 5: C

HOẠT ĐỘNG VẬN DỤNG

GV yêu cầu HS thảo luận cặp đôi, hoàn thành hai bài tập sau:

Bài 1: Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện số lượng vi khuẩn tăng thêm 25% sau mỗi hai ngày.

a) Công thức P(t) = P₀.a^t cho phép tính số lượng vi khuẩn của mẻ nuôi cấy sau t ngày kể từ thời điểm ban đầu. Xác định các tham số P₀ và a (a > 0). Làm tròn a đến hàng phần trăm.

b) Sau 5 ngày, số lượng vi khuẩn là bao nhiêu? Làm tròn kết quả đến hàng trăm.

c) Sau bao nhiêu ngày thì số lượng vi khuẩn gấp đôi số lượng ban đầu? Làm tròn kết quả đến một chữ số thập phân.

Bài 2: Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức pH = − log [H⁺], trong đó [H⁺] là nồng độ H⁺ của dung dịch đó tính bằng mol/L. Nồng độ H⁺ trong dung dịch cho biết độ acid của dung dịch đó.

a) Dung dịch A có độ pH là 1,9 và dung dịch B có độ pH là 2,5. Dung dịch nào có độ acid cao hơn và độ acid cao hơn bao nhiêu lần?

b) Nước cất có nồng độ H⁺ là 10^–7 mol/L. Nước chảy từ một vòi nước có độ pH từ 6,5 đến 6,7 thì có độ acid cao hay thấp hơn nước cất.