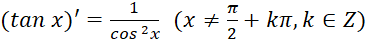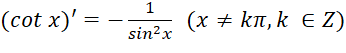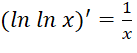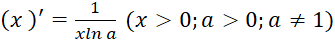Slide bài giảng Toán 11 chân trời Chương 7 Bài 2: Các quy tắc tính đạo hàm
Slide điện tử Bài 2: Các quy tắc tính đạo hàm. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 11 Chân trời sáng tạo sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 2. CÁC QUY TẮC ĐẠO HÀM (5 TIẾT)
HOẠT ĐỘNG KHỞI ĐỘNG
GV yêu cầu HS thảo luận và trả lời:
Giả sử hàm số f(x) và g(x) lần lượt có đạo hàm tại x0 là f'(x0) và g'(x0). Làm thế nào để tính đạo hàm của các hàm số là tổng, hiệu, tích hoặc thương của f(x) và g(x) tại x0?
Ví dụ: Hãy tính đạo hàm của hàm số: C + ![]() ?
?
- GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
NỘI DUNG BÀI HỌC GỒM
- Đạo hàm của hàm số
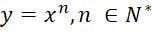
- Đạo hàm của hàm số y =
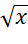
- Đạo hàm của hàm số lượng giác
- Đạo hàm
- Đạo hàm của tổng, hiệu, tích, thương của hai hàm số
- Đạo hàm của hàm hợp
- Đạo hàm cấp hai
- Luyện tập
- Vận dụng
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. ĐẠO HÀM CỦA HÀM SỐ ![]()
Hoạt động 1: Tìm hiểu đạo hàm của hàm số ![]()
Nêu quy tắc đạo hàm của hàm số y = xn.
Nội dung ghi nhớ:
Quy tắc
Hàm số ![]() với
với ![]() có đạo hàm trên
có đạo hàm trên ![]() và
và ![]() .
.
2. ĐẠO HÀM CỦA HÀM SỐ Y = ![]()
Hoạt động 2: Tìm hiểu đạo hàm của hàm số y = ![]()
Nêu quy tắc tính đạo hàm của hàm căn thức.
Nội dung ghi nhớ:
Quy tắc
Hàm số ![]() có đạo hàm trên khoảng
có đạo hàm trên khoảng ![]() và
và 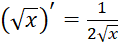 .
.
3. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
Hoạt động 3: Tìm hiểu đạo hàm của hàm số lượng giác
Định nghĩa tính đạo hàm của các hàm số: cos x; tan x; cot x.
Nội dung ghi nhớ:
Quy tắc
4. ĐẠO HÀM
Hoạt động 4: Tìm hiểu đạo hàm
Nêu quy tắc tính đạo hàm của hàm số mũ và hàm số lôgarit.
Nội dung ghi nhớ:
Quy tắc
5. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG CỦA HAI HÀM SỐ
Hoạt động 5: Tìm hiểu đạo hàm của tổng, hiệu, tích, thương của hai hàm số
Nêu quy tắc tính đạo hàm của tổng, hiệu, tích, thương của hai hàm số
Nội dung ghi nhớ:
Quy tắc
Cho hai hàm số ![]() có đạo hàm tại điểm
có đạo hàm tại điểm ![]() thuộc tập xác định. Ta có:
thuộc tập xác định. Ta có:
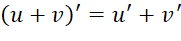
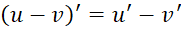
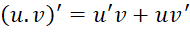 (1)
(1)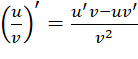 (với
(với 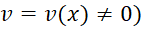 (2)
(2)
6. ĐẠO HÀM CỦA HÀM HỢP
Hoạt động 6: Tìm hiểu đạo hàm của hàm hợp
Nêu định nghĩa, quy tắc tính đạo hàm của hàm hợp.
Nội dung ghi nhớ:
Định nghĩa hàm hợp
Cho ![]() là hàm số của
là hàm số của ![]() xác định trên khoảng
xác định trên khoảng ![]() và lấy giá trị trên khoảng
và lấy giá trị trên khoảng ![]() ;
; ![]() là hàm số của
là hàm số của ![]() xác định trên khoảng
xác định trên khoảng ![]() và lấy giá trị trên
và lấy giá trị trên ![]() . Ta lập hàm số xác định trên
. Ta lập hàm số xác định trên ![]() và lấy giá trị trên
và lấy giá trị trên ![]() theo quy tắc sau:
theo quy tắc sau: ![]() .
.
Hàm số ![]() được gọi là hàm hợp của hàm số
được gọi là hàm hợp của hàm số ![]() với
với ![]() .
.
Quy tắc
Cho hàm số ![]() có đạo hàm tại
có đạo hàm tại ![]() là
là ![]() và hàm số
và hàm số ![]() có đạo hàm
có đạo hàm ![]() là
là ![]() thì hàm hợp
thì hàm hợp ![]() có đạo hàm tại
có đạo hàm tại ![]() là
là ![]() .
.
7. ĐẠO HÀM CẤP HAI
Hoạt động 7: Tìm hiểu đạo hàm cấp hai
Nêu định nghĩa, ý nghĩa cơ học của đạo hàm cấp hai
Nội dung ghi nhớ:
Định nghĩa
Cho hàm số ![]() có đạo hàm
có đạo hàm ![]() tại mọi
tại mọi ![]() .
.
Nếu hàm số ![]() có đạo hàm tại
có đạo hàm tại ![]() thì ta gọi đạo hàm của
thì ta gọi đạo hàm của ![]() là đạo hàm cấp hai của hàm số
là đạo hàm cấp hai của hàm số ![]() tại
tại ![]() , kí hiệu
, kí hiệu ![]() hoặc
hoặc ![]() .
.
Ý nghĩa cơ học của đạo hàm cấp hai
Đạo hàm cấp hai ![]() là gia tốc tức thời tại thời điểm
là gia tốc tức thời tại thời điểm ![]() của vật chuyển động có phương trình
của vật chuyển động có phương trình ![]() .
.
HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Cho hàm số f(x)=(x+10)6. Tính f''(2):
A. 608092
B. 610202
C. 630880
D. 622080
Câu 2: Đạo hàm cấp hai của hàm số y=cos2x
A. −2cos2x
B. −cos4x
C. cos2x
D. 2cosx
Câu 3: Một nhà sản xuất máy ảnh ước tính khi x (trăm) máy ảnh được sản xuất thì tổng lợi nhuận thu được sẽ là:
P(x)=−0,0035x3+0,07x2+25x−200 (nghìn đô). Tính P'(10) và giải thích kết quả nhận được.
A. P'(10) = 25,35; lợi nhuận tăng xấp xỉ 25,35 nghìn đô khi mức sản xuất tăng từ 10 000 lên 11 000 máy ảnh
B. P'(10) = 5,75; lợi nhuận tăng xấp xỉ 5,75 nghìn đô khi mức sản xuất tăng từ 10 000 lên 11 000 máy ảnh
C. P'(10) = 20,45; lợi nhuận tăng xấp xỉ 20,45 nghìn đô khi mức sản xuất tăng từ 10 000 lên 11 000 máy ảnh
D. P'(10) = 15,15; lợi nhuận tăng xấp xỉ 15,15 nghìn đô khi mức sản xuất tăng từ 10 000 lên 11 000 máy ảnh
Câu 4: Cho hàm số y=mx4+(m2−9)x2+10. Tìm m để phương trình y' = 0 có ba nghiệm phân biệt
A. m < -3
B. 0 < m < 3
C. -3 < m < 0
D. A và B đều đúng
Câu 5: Đạo hàm của hàm số y = cos25x:
A. y′=10sin5x
B.y′=−10sin5x
C. y′=−5sin10x
D. y′=5sin10x
Nội dung ghi nhớ:
Câu 1: D
Câu 2: A
Câu 3: A
Câu 4: D
Câu 5: C
HOẠT ĐỘNG VẬN DỤNG
Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:
Câu 1: Một công ty xác định rằng tổng chi phí của họ, tính theo nghìn đô-la, để sản xuất x mặt hàng là C(x) = ![]() và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t + 40. Sau 4 tháng, chi phí sẽ tăng nhanh thế nào kể từ khi công ty thực hiện kế hoạch đó?
và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t + 40. Sau 4 tháng, chi phí sẽ tăng nhanh thế nào kể từ khi công ty thực hiện kế hoạch đó?
Câu 2: Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,81t2, trong đó t là thời gian được tính bằng giây và s tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tính:
a) Quãng đường vật đã rơi sau 2 giây; b) Gia tốc của vật sau 2 giây.