Slide bài giảng Toán 11 chân trời Bài tập cuối chương 3

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG III

BÀI TẬP TỰ LUẬN

Bài 6 (Trang 86):

Tìm các giới hạn sau:

a)
b)
c)
d)

Trả lời rút gọn: 

a) ;
b) ;
c) ;
d) .

Bài 7 (Trang 86):

Cho tam giác đều có cạnh bằng a, gọi là tam giác H₁. Nỗi các trung điểm của H₁ để tạo thành tam giác H₂. Tiếp theo, nối các trung điểm của H₂ để tạo thành tam giác H₃ (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác H₁, H₂, H₃, ...

Tỉnh tổng chu vi và tổng diện tích của các tam giác của dãy.

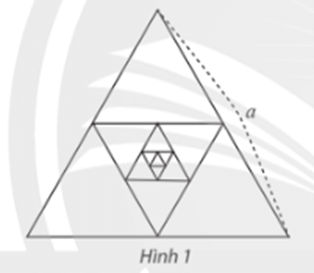
Trả lời rút gọn: 

Gọi là độ dài cạnh của tam giác .
Ta có
Chu vi của tam giác là ; diện tích của tam giác là .

Tổng chu vi của các tam giác là:

Tổng diện tích các tam giác là:

S

Bài 8 (Trang 86):

Tìm các giới hạn sau:

a)
b)
c)

Trả lời rút gọn: 

a) ;
b) ;
c)

Bài 9 (Trang 86):

Tìm các giới hạn sau:

a)
b)

Trả lời rút gọn: 

a) ;
b) .

Bài 10 (Trang 86):

Tìm các giới hạn sau:

a)

b)

Trả lời rút gọn: 

a) (vì
b) (vì

Bài 11 (Trang 86):

Xét tính liên tục của hàm số f(x) = .

Trả lời rút gọn: 

Suy ra: 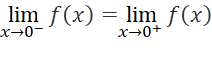Hay f(x) liên tục tại x = 0

Vậy hàm số liên tục trên .

Bài 12 (Trang 86):

Cho hàm số f(x) = . Tìm a để hàm số y = f(x) liên tục trên ℝ.

Trả lời rút gọn: 

Để f(x) liên tục trên thì f(x) liên tục tại . Hay

Vậy a =10.

Bài 13 (Trang 86):

Trong một tủ thí nghiệm, nhiệt độ trong tủ sấy được điều khiển tăng từ 10°C, mỗi phút tăng 2°C trong 60 phút, sau đó giảm mỗi phút 3°C trong 40 phút. Hàm số biểu thị nhiệt độ (tính theo ºC) trong tủ theo thời gian t (tính theo phút) có dạng

T(t) = (k là hằng số).

Biết rằng T(t) là hàm liên tục trên tập xác đinh. Tìm giá trị của k.

Trả lời rút gọn: 

Hàm số liên tục tại các điểm và .
.
Để hàm số liên tục tại , ta phải có , suy ra 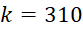.