Slide bài giảng Toán 11 chân trời Chương 4 Bài 5: Phép chiếu song song

Tóm lược nội dung

BÀI 5: PHÉP CHIẾU SONG SONG

1. KHÁI NIỆM PHÉP CHIẾU SONG SONG

Khám phá 1 (Trang 121):

Trong hoạt động khởi động:

a) Các tia sáng AA’, BB’, DD’ có song song với nhau hay không?

b) Nêu cách xác định bóng C’ của điểm C trên mặt đường.

Trả lời rút gọn: 

a) Các tia sáng AA', BB', DD' song song với nhau.

b) Qua C kẻ đường thẳng song song với AA’ và cắt mặt đường tại C'. Ta được bóng C' của điểm C trên mặt đường.

Thực hành 1 (Trang 122):

Tìm phương chiếu, mặt phẳng chiếu của phép chiếu song song được mô tả trong Hình 2.

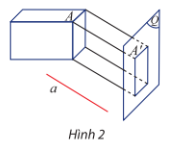
Trả lời rút gọn: 

Phương chiếu a, mặt phẳng chiếu (Q).

Vận dụng 1 (Trang 122):

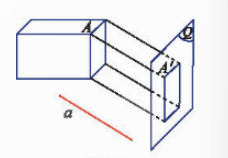
Tìm ảnh của hình hộp ABEF.DCGH qua phép chiếu song song được mô tả trong Hình 3.

Trả lời rút gọn: 

Ảnh của hình hộp ABEF.DCGH qua phép chiếu theo phương là những hình bình hành: A’B’C’D’, A’F’H’D’, A’B’E’F’, E’B’C’G’, H’G’C’D’, H’G’E’F’.

2. CÁC TÍNH CHẤT CƠ BẢN CỦA PHÉP CHIẾU SONG SONG

Khám phá 2 (Trang 122):

Trong Hình 4, xét phép chiếu theo phương l lên mặt phẳng (P), mặt phẳng (Q) chứa đường thẳng a và song song với phương chiếu.

a) Khi điểm M thay đổi trên đường thẳng a thì ảnh M’ của nó thay đổi ở đâu?

b) Từ đó hãy chỉ ra ảnh của đường thẳng a qua phép chiếu theo phương l lên mặt phẳng (P).

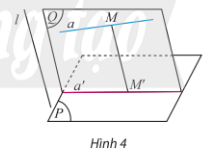
Trả lời rút gọn: 

a) Khi M thay đổi trên đường thẳng a thì M' thay đổi trên đường thẳng a'.

b) Ảnh của đường thẳng a theo phép chiếu theo phương l trên mặt phẳng (P) là đường thẳng a'.

Khám phá 3 (Trang 123):

Trong Hình 5, xét phép chiếu theo phương l với mặt phẳng chiếu (P). Biết a // b với a ⊂ (Q) và b ⊂ (R). Nêu nhận xét về vị trí tương đối của hình chiếu a’, b’ của a, b trong hai trường hợp: (Q) // (R); (Q) ≡ (R).

Trả lời rút gọn: 

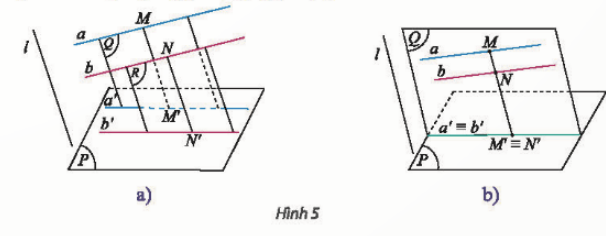
Nếu (Q)//(R) thì a'//b

Nếu (Q)≡(R) thì a′≡b′.

Thực hành 2 (Trang 124):

Cho hình thang ABCD có đáy lớn AB và AB = 2CD, hình chiếu song song của ABCD là tứ giác A’B’C’D’. Chứng minh rằng A’B’C’D’ cũng là một hình thang và A’B’ = 2C’D’.

Trả lời rút gọn: 

Ta có , suy ra là trung điểm của , ta có , suy ra là trọng tâm tam giác . 

Vận dụng 2 (Trang 124):

Cho G là trọng tâm tam giác ABC, M là trung điểm BC và hình chiếu song song của tam giác ABC là tam giác A’B’C’. Chứng minh rằng hình chiếu M’ của M là trung điểm của B’C’ và hình chiếu G’ của G cũng là trọng tâm tam giác A’B’C’.

Trả lời rút gọn: 

Ta có , suy ra là trung điểm của , ta có , suy ra là trọng tâm tam giác . 

3. HÌNH BIỂU DIỄN CỦA MỘT HÌNH KHÔNG GIAN

Khám phá 4 (Trang 124):

Quan sát Hình 7 và cho biết các tia nắng song song đã tạo ra hình chiếu của hình hộp như thế nào trên nền nhà.

Trả lời rút gọn: 

Các mặt của hình hộp có hình chiếu là các hình bình hành.

Thực hành 3 (Trang 126):

Gọi tên các hình khối có hình biểu diễn là các hình trong Hình 10.

Trả lời rút gọn: 

a) Hình hộp

b) Hình lăng trụ tam giác

c) Hình chóp có tứ giác.

Vận dụng 3 (Trang 126):

Vẽ hình biểu diễn của một hình chóp tam giác SABC đặt trên một hình lăng trụ tam giác ABC.A’B’C’.

Trả lời rút gọn: 

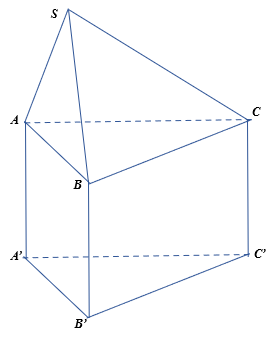4. BÀI TẬP CUỐI SGK 

Bài 1 (Trang 126):

Trong các mệnh đề sau, mệnh đề nào đúng?

a) Một đường thẳng có thể song song với hình chiếu của nó;

b) Một đường thẳng có thể trùng với hình chiếu của nó;

c) Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau;

d) Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.

Trả lời rút gọn: 

a) Đúng, 

b) Đúng,

c) Đúng

d) Sai.

Bài 2 (Trang 126):

Vẽ hình biểu diễn của một lục giác đều

Trả lời rút gọn

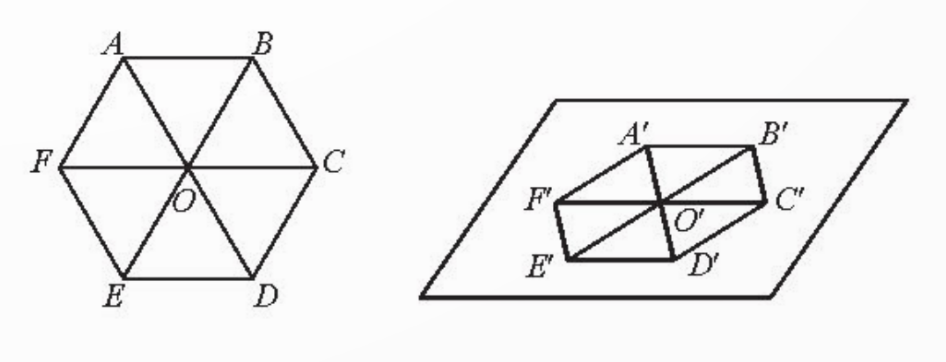
Do phép chiếu song song bảo toàn tính cùng phương và tỉ số của các đoạn thẳng cùng phương nên hình biểu diễn của lục giác đều phải thoả mãn:

+ Các đoạn song song và bằng nhau.

+ Các đoạn song song và bằng nhau.

+ Các đoạn song song và bằng nhau.

Để vẽ hình biễu diễn của lục giác đều tâm , ta thực hiện các bước sau:

+ Vẽ hình bình hành biểu diễn hình bình hành .

+ Vẽ lần lượt đối xứng với qua .

Ta được là hình biễu diễn của lục giác đều .

Bài 3 (Trang 126):

Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn

Trả lời rút gọn: 

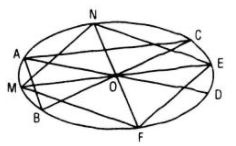
Do phép chiếu song song bảo toàn tính cùng phương và tỉ số của các đoạn thẳng cùng phương nên hình biểu diễn của hình vuông nội tiếp hình tròn tâm phải thoả mãn:

+) là hình bình hành có các đỉnh nằm trên elip tâm , với elip tâm là hình biểu diễn của hình tròn tâm .

+) Đường chéo của hình bình hành đi qua trung điểm của các dây , vói song song .

Để vẽ hình biểu diễn của hình vuông nội tiếp hình tròn tâm ta thực hiện các bước sau:

+ Vẽ elip tâm biểu diễn hình tròn tâm

+ Vẽ đường kính đi qua tâm của elip biểu diễn đường chéo của hình vuông.

+ Vẽ dây cung song song với .

+ Vẽ trung điểm của .

+ Vẽ đường kính của elip đi qua và biểu diễn đường chéo của hình vuông.

Ta được hình biễu diễn của hình vuông nội tiếp hình tròn tâm .

Bài 4 (Trang 126):

Cho hai điểm A, B nằm ngoài mặt phẳng (α) và đường thẳng d cắt (α). Giả sử đường thẳng AB cắt (α) tại điểm O. Gọi A’ và B’ lần lượt là hình chiếu song song của A và B trên (α) theo phương của đường thẳng d. Ba điểm O, A’, B’ có thẳng hàng không? Vì sao? Chọn d sao cho:

a) A’B’ = AB;

b) A’B’ = 2AB.

Trả lời rút gọn: 

Gọi là mặt phẳng chứa đường thẳng và các đường song song và . Ta có là các điễm chung của hai mặt phẳng và , ba điểm này phải nằm trên giao tuyến của hai mặt phẳng và nên chúng thẳng hàng.

a) Trên mặt phẳng , vẽ đường thẳng đi qua . Trên lấy điểm sao cho .

Chọn là đường thẳng đi qua . Ta có , suy ra . Vậy .

.

Chọn là đường thẳng đi qua . Ta có , suy ra . Vậy .

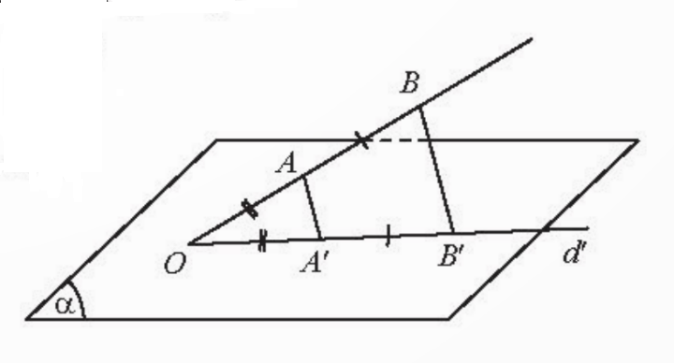
b) Trên mặt phẳng vẽ dường thẳng di qua . Trên lấy điểm sao cho .

Chọn là đường thẳng đi qua . Ta có , suy ra . Vậy .

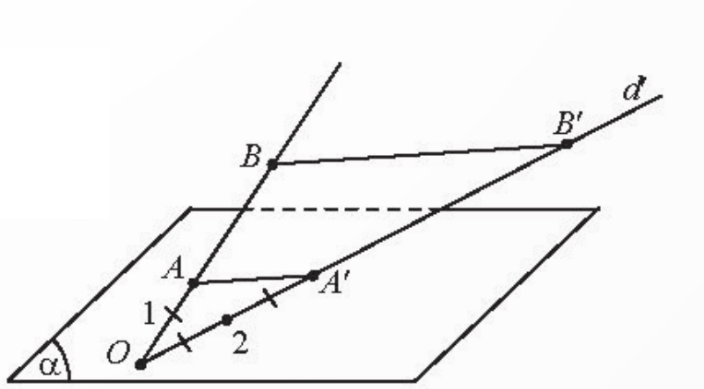
Bài 5 (Trang 126):

Vẽ hình biểu diễn của:

a) Hình lăng trụ có đáy là tam giác đều;

b) Hình lăng trụ có đáy là lục giác đều;

c) Hình hộp.

Trả lời rút gọn: 

a)

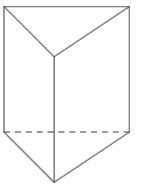
b)

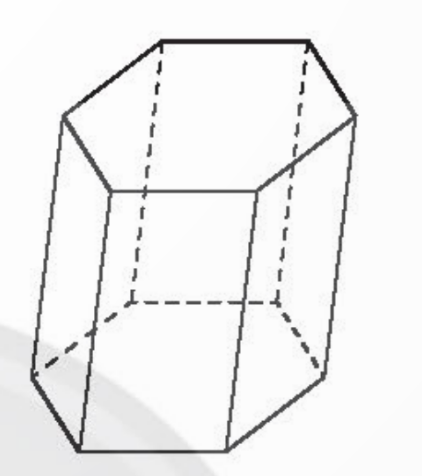
c)