Giải Câu 46 Bài 9: Thể tích của hình chóp đều sgk Toán 8 tập 2 Trang 124
Câu 46: Trang 124 - SGK Toán 8 tập 2
S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:
a) Diện tích đáy và thể tích của hình chóp (biết $\sqrt{108}\approx 10,39$);
b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết $\sqrt{1333}\approx 36,51$).

a) Tam giác HMN là tam giác đều.
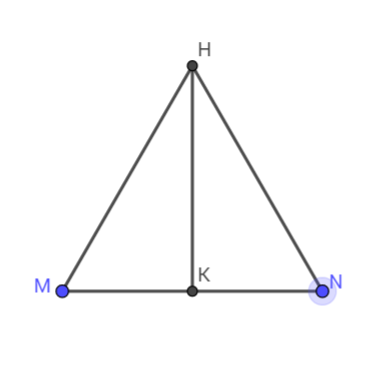
Gọi K là trung điểm MN.
=> HK là đường cao trong tam giác HMN.
=> \(HK = \sqrt{HM^{2}- KM^{2}}= \sqrt{12^{2}- 6^{2}}= \sqrt{108} \approx 10,39(cm)\)
- Diện tích đáy của hình chóp lục giác đều chính là 6 lần diện tích của tam giác đều HMN.
Nên \(S_{đ}= 6.\frac{1}{2}. MN.HK = 6.\frac{1}{2}. 12 .10,39 = 374,04(cm^2)\)
- Thể tích của hình chóp:
\(V = \frac{1}{3}. S_{đ}. SH = \frac{1}{3}. 374,04 . 35 = 4363,8(cm^3)\)
b) Ta có:
\(SM=\sqrt{SH^{2}+ MH^{2}}= \sqrt{35^{2}+ 12^{2}} = \sqrt1369 = 37 (cm)\)
Đường cao của mỗi mặt bên là:
\(h = SK = \sqrt{SM^{2}- KM^{2}}= \sqrt{37^{2}- 6^{2}} = \sqrt1333 ≈ 36,51 (cm)\)
Diện tích xung quanh hình chóp là :
\(S_{xq}= \frac{1}{2}. p.d = \frac{1}{2} .6. MK .SK = \frac{1}{2}.6.12. 36,51 = 1314,36(cm^2)\)
Diện tích toàn phần: $S_{tp}= S_{xq}+ S_{đ}= 1314,36 + 374,04 = 1688,4(cm^2)$

Bình luận