Giải Câu 45 Bài 9: Thể tích của hình chóp đều sgk Toán 8 tập 2 Trang 124

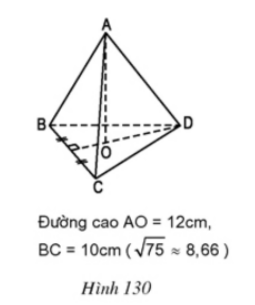
Hình 130

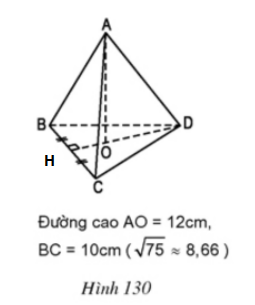
Gọi H là trung điểm BC.

Vì tam giác BCD là tam giác đều => HD đồng thời là đường cao của tam giác BCD.

Ta có: $HB=HC=\frac{1}{2}.BC=\frac{1}{2}.10=5(cm)$

Mặt khác: $HD^+HC^2=CD^2$ (định lý Pitago trong tam giác vuông HCD)

=> $HD=\sqrt{CD^2-HC^2}=\sqrt{10^2-5^2}=\sqrt{100-25}=\sqrt{75}\approx 8,66(cm)$

Vậy

• Diện tích đáy của hình chóp đều là:

$S = \frac{1}{2}.BC.HD = \frac{1}{2}. 10. 8,66 = 43,3(cm^2)$

• Thể tích hình chóp đều là:

$V =\frac{1}{3}. S. AO = \frac{1}{3}. 43,3 .12 = 173,2(cm^3)$

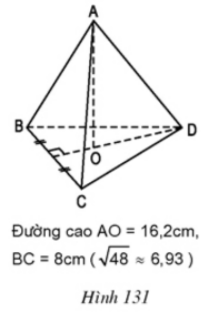
Hình 131

Tương tự hình 130, ta có: HD là đường cao của tam giác đều BDC.

=> $HD= \sqrt{DC^{2}- (\frac{BC}{2})^{2}}= \sqrt{8^{2}- 4^{2}} = \sqrt{48} \approx 6,93(cm)$

Vậy

• Diện tích đáy của hình chóp đều là:

$S = \frac{1}{2}.BC.HD = \frac{1}{2}.8.6,93 = 27,72(cm^2)$

• Thể tích hình chóp đều là:

$V = \frac{1}{3}. S.  AO = \frac{1}{3}. 27,72. 16,2 =149,69(cm^3)$