Giải Câu 33 Bài 6: Trường hợp đồng dạng thứ hai sgk Toán 8 tập 2 Trang 77

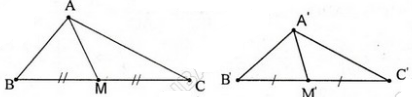
Giả sử ∆A'B'C' ∽ ∆ABC theo tỉ số k và AM, A'M' là hai đường trung tuyến tương ứng của hai tam giác $\Delta ABC;\,\ \Delta A'B'C'$.

 Vì ∆A'B'C' ∽ ∆ABC => \(\widehat{B}= \widehat{B'}\) và \(\frac{A'B'}{AB} = \frac{B'C'}{BC}\).

Từ: \(\frac{A'B'}{AB} = \frac{B'C'}{BC}\) mà $B'C' = 2B'M',;\,\ BC = 2BM$

=> \(\frac{A'B'}{AB} = \frac{2.B'M'}{2.BM}=\frac{B'M'}{BM}\)

Xét  ∆ABM và ∆A'B'M' có: \(\widehat{B}= \widehat{B'};\,\ \frac{AB}{A'B'}=\frac{AM}{A'M'}\)

=> ∆A'B'M' ∽ ∆ABM => \(\frac{A'M'}{AM}= \frac{A'B'}{AB} = k\).