Đáp án câu 5 đề 10 kiểm tra học kì II toán 8

Câu 5

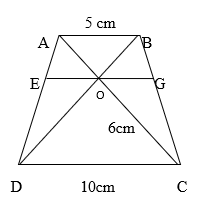
a) ∆AOB∼∆COD (g.g)

$\Rightarrow\frac{OA}{OC}$ = $\frac{OB}{OD}\ \Rightarrow OA.OD$ = $OC.PB$

b) Từ câu a suy ra $\frac{OA}{OC}$ = $\frac{OB}{OD}$ = $\frac{AB}{CD}$

$\Rightarrow \frac{OA}{6}$ = $\frac{5}{10}$

$\Rightarrow OA$ = $\frac{6.5}{10}$ = $3$cm

Do  OE $\parallel$ DC nên theo hệ quả định lí Talet:

$\frac{AE}{AC}$ = $\frac{AO}{AC}$ = $\frac{EO}{DC}$

$\Leftrightarrow \frac{3}{3+6\} = $\frac{EO}{10}$

$\Leftrightarrow EO$ = $\frac{3.10}{9}$ = $\frac{30}{9}$ = $\frac{10}{3}$ cm

c) OE $\parallel$ AB, theo hệ quả định lý Talet ta có: $\frac{OE}{AB}$ = $\frac{DE}{DA}\left(1\right)$

* OE $\parallel$ CB, theo hệ quả định lý Talet ta có: $\frac{OE}{DC}$ = $\frac{AE}{DA}\left(2\right)$

Cộng vế với vế của (1) và (2) ta được: $\frac{OE}{AB}+\frac{OE}{DC}$ = $\frac{DE}{DA}+\frac{AE}{DA}$ = $1$

$\Rightarrow OE\left(\frac{1}{AB}+\frac{1}{CD}\right)$ = $1$ hay $\frac{1}{OE}$ = $\frac{1}{AB}+\frac{1}{CD}$

Chứng minh tương tự ta có $\frac{1}{OG}$ = $\frac{1}{AB}+\frac{1}{DC}$