Đáp án câu 4 đề 7 kiểm tra học kì II toán 8

Câu 4
 
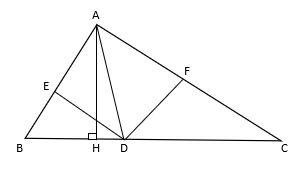
a) Xét $\bigtriangleup HBA$ và $\bigtriangleup ABC$ có :

+) $\widehat{AHB}$ = \widehat{BAC} = $90^{\circ}$

+) $\widehat{ABC}$ chung

$\Rightarrow $ $\bigtriangleup HBA \sim \bigtriangleup ABC$

b) Áp dụng định lý Pitago trong tam giác ABC ta có: 

$BC^{2}$ = $AB^{2}$ + $AC^{2}$ = $12^{2}$ + $16^{2}$ = 400

$\Rightarrow $ $BC$ = $20$

Ta có $\bigtriangleup HBA \sim \bigtriangleup ABC$ 

$\Rightarrow $ $\frac{AB}{BC}$ = $\frac{AH}{AC}$  $\Rightarrow $ $\frac{12}{20}$ = $\frac{AH}{16}$

$\Rightarrow AH$ = $\frac{12.16}{20}$ = $9,6$ cm

c) $\frac{EA}{EB}$ = $\frac{DA}{DB}$ (vì DE là tia phân giác của ADB) 

$\frac{FC}{FA}$ = $\frac{DC}{DA}$  (vì DF là tia phân giác của ADC) 

$\Rightarrow $ $\frac{EA}{EB}$ . $\frac{FC}{FA}$ = $\frac{DA}{DB}$ . $\frac{DC}{DA}$ = $\frac{DC}{DB}$ (1) 

(1) $\Rightarrow $ $\frac{EA}{EB}$ . $\frac{FC}{FA}$ . $\frac{DB}{DC}$ = $\frac{DB}{DC}$ . $\frac{DC}{DB}$ = 1 (đpcm)