Câu 1: Trong những biểu thức sau, biểu thức nào là đơn thức nhiều biến? 

• A. $\frac{x}{y}$

• B. 4xy + 1

• C. 3$x^{2}$yz
• D. 2 - $\sqrt{x}$

Câu 2:  Đáy của hình chóp tứ giác đều là hình ?

• A.Hình bình hành
• B.Hình chữ nhật 
• C.Hình thoi

• D.Hình vuông

Câu 3: Tam giác nào là tam giác đều trong các tam giác có độ dài ba cạnh như sau?

• A. 3; 4; 5

• B. 6; 6; 6

• C. 6; 8; 6
• D. 10; 15; 20

Câu 4: Điền vào chỗ chấm sau: $x^{2}$ - … = (x - 4)(x + 4)

• A. 16

• B. 10
• C. 2
• D. 8

Câu 5: Phân thức $\frac{A}{B}$ khác định khi nào?

• A. A = 0
• B. B = 0
• C. A # 1

• D. B # 0

Câu 6: Nghịch đảo của phân thức $\frac{2x + 1}{x + 2}$ với x khác - $\frac{1}{2}$ và x khác - 2

• A. - $\frac{2x + 1}{x + 2}$
• B. - $\frac{x + 2}{2x + 1}$

• C. $\frac{x + 2}{2x + 1}$

• D. - $\frac{x + 2}{2x + 1}$

Câu 7: Hằng đẳng thức $A^{2}$ - $B^{2}$=(A−B)(A+B) có tên là

• A. Bình phương của một tổng;
• B. Bình phương của một hiệu;
• C. Tổng hai bình phương;

• D. Hiệu hai bình phương.

Câu 8: Cho P = $\frac{2x - 1}{x + 2}$ tại x = 3. Giá trị của P là: 

• A. 1

• B. -1
• C. -5
• D. 5

Câu 9: Mặt bên SAB của hình chóp tam giác đều S.ABC là:

• A. Tam giác cân tại A 
• B. Tam giác cân tại B
• C. Tam giác vuông

• D. Tam giác đều

Câu 10: Triển khai biểu thức sau $(x - 1)^{2}$:

• A. $x^{2}$ + x - 1
• B. $x^{2}$ - x + 1
• C. $x^{2}$ - 2x - 1

• D. $x^{2}$ - 2x + 1

Câu 11: Kết quả của phép tính 15$x^{2}$$y^{2}$z : (3xyz) là: 

• A. 5xy

• B. 5$x^{2}$$y^{2}$z
• C. 5xyz
• D. 15xy

Câu 12: Nếu hai biểu thức A và B nhận giá trị như nhau với … của biến thì ta nói A = B là một …. Hãy điền vào chỗ “…” để được khẳng định đúng. 

• A. một số giá trị; hằng đẳng thức
• B. một giá trị; hằng đẳng thức 
• C. vài giá trị; đồng nhất thức 

• D. mọi giá trị; đồng nhất thức 

Câu 13: Cho hình vẽ dưới đây. Khẳng định nào sau đây là sai? 

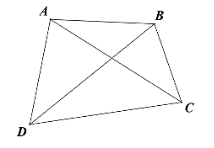
• A. Hai đỉnh kề với đỉnh A là B và D
• B. Tứ giác ABCD có 2 đường chéo 

• C. Các cạnh của tứ giác là AB, BC, CD, DA, AC, BD

• D. Hai điểm đối nhau là A và C; B và D

Câu 14: Phân tích đa thức $x^{2}$ - 6x + xy - 6y thành nhân tử: 

• A. (x - y) (y - 6)
• B. (x - y)(x - 6)

• C. (x + y)( x - 6)

• D. (x + y)(y - 6)

Câu 15: Tích của hai đơn thức $\frac{1}{2}$x$y^{3}$ và x(--8y)x$z^{2}$ có phần hệ số là: 

• A. - 7

• B. - 4

• C. 4
• D. 7

Câu 16: Trong các phát biểu sau, phát biểu nào đúng . Chiều cao của hình chóp tam giác đều là?

• A. Chiều cao của mặt đáy.
• B. Độ dài đường trung tuyến của một mặt bên của hình chóp .

• C. Độ dài đoạn thẳng nối từ đỉnh tới trọng tâm của tam giác đáy. 

• D. Độ dài đoạn thẳng nối từ đỉnh hình chóp tới trung điểm của một cạnh đáy.

Câu 17: Cho hình chóp tam giác S.ABC  đều như hình vẽ sau, mặt đáy của hình chóp là:

• A. ABC

• B. SBC
• C. SAB 
• D. SAC

Câu 18: Tìm x thỏa mãn  $\frac{3x + 15}{$x^2$ - 4}$ :  $\frac{x + 5}{x - 2}$ = 1 (x # 2; x # -2; x # -5)

• A. x = 1

• B. x = -1
• C. x = 0
• D. x = 3

Câu 19: Đa thức - 4$x^{2}$ + 12x - 9 được viết thành: 

• A. (2x - 3)(2x + 3)

• B.- $(2x - 3)^{2}$

• C. - $(2x + 3)^{2}$
• D.  $(3 - 2x)^{2}$

Câu 20: Thực hiện phép tính 7$x^{2}$ (5$x^{3}$  + 3$x^{4}$) được kết quả là: 

• A. 35$x^{5}$  + 21$x^{6}$ 

• B. 35$x^{6}$  + 21$x^{5}$ 
• C. 35$x^{5}$  - 21$x^{6}$ 
• D. 35$x^{6}$  + 21$x^{5}$ 

Câu 21: Hình nào sau đây là hình chóp tam giác đều?

• A. Hình có đáy là tam giác đều;
• B. Hình có đáy là tam giác;
• C. Hình có đáy là tam giác đều và tất cả các cạnh đều vuông góc với mặt đáy;

• D. Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.

Câu 22: Cho hình chóp tứ giác đều S. ABCD như hình. Gọi O là giao điểm hai đường chéo AC và BD, khi đó SO là:

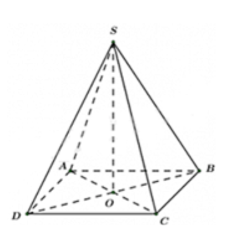
• A. Cạnh bên của hình chóp tứ giác đều
• B. Cạnh trong của hình chóp tứ giác đều

• C. Đường cao của hình chóp tứ giác đều

• D. Trung tuyến của hình chóp tứ giác đều

Câu 23: Cho hình chóp tứ giác đều như hình vẽ sau, chọn khẳng định đúng:

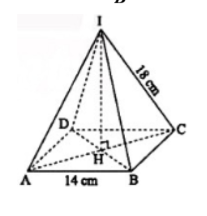
• A. AD = 18cm

• B. BC = 14cm 

• C. IC = IH
• D. IC = BC