TRẮC NGHIỆM

Câu 1: Cho đa giác 9 cạnh, số đường chéo của đa giác đó là:

• A. 36              

• B. 27              

• C. 20              
• D. 18

Câu 2: Tổng số đo các góc của đa giác đều 7 cạnh là:

• A. 900⁰           

• B. 540⁰           
• C. 1080⁰         
• D. 108⁰

Câu 3: Mỗi góc trong của lục giác đều là:

• A. 120⁰           

• B. 150⁰           
• C. 90⁰
• D. 135⁰

Câu 4: Tổng số đo các góc của hình đa giác n cạnh là 1620⁰ thì số cạnh n là:

• A. n = 9          
• B. n = 10        

• C. n = 11        

• D. n = 8

Câu 5: Cho ABCDEF là hình lục giác đều. Hãy chọn câu sai:

• A. ABCDEF có một tâm đối xứng                
• B. Mỗi góc trong của nó là 120⁰.
• C. Tổng các góc trong của nó là 720⁰.                                  

• D. Mỗi góc trong của nó là 150⁰.

Câu 6: Số đo mỗi góc trong và ngoài của ngũ giác đều là:

• A. 75⁰; 150⁰   
• B. 108⁰; 72⁰    

• C. 100⁰; 80⁰                

• D. 110⁰; 70⁰

Câu 7: Số đường tròn nội tiếp của một đa giác đều là

• A. 1

• B. 2
• C. 3
• D. 0

Câu 8: Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O. Tính số đo góc AOB

• A. 60°

• B. 120°
• C. 30°
• D. 240°

Câu 9: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là giao điểm hai đường cao BD và CE của tam giác ABC (D ∈ AC, E ∈ AB). ) Đường thẳng AO cắt ED và BD lần lượt tại K và M. Tìm khẳng định đúng nhất?

• A. Tứ giác ADHE nội tiếp trong một đường tròn.
• B. AK.AM = AD²
• C.  C. 

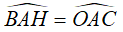
• D. Tất cả đúng

Câu 10: Cho ∆ABC cân tại A có Cho ∆ABC cân tại A có = 120^o. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy D sao cho BCD là tam giác đều. Khi đó: = 120^o. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy D sao cho BCD là tam giác đều. Khi đó:

• A. ∆ACD cân                                  

• B. ABDC nội tiếp

• C. ABDC là hình thang                     
• D. ABDC là hình vuông

Câu 11: Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính 5cm (làm tròn đến chữ số thập phân tứ nhất).

• A. 7,26cm  

• B. 7,3cm    

• C. 7,2cm    
• D. 13,7cm

Câu 12: Cho (O; 4) có dây AC bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp đường tròn đó (điểm C và A nằm cùng phía với BO). Tính số đo góc ACB

• A. 30^o         
• B. 45^o         
• C. 60^o         

• D. 15^o

Câu 13: Cho ngũ giác đều ABCDE. Gọi K là giao điểm của AC và BE. Khi đó hệ thức nào dưới đây là đúng?

• A. CB² = AK. AC                             

• B. OB² = AK. AC
• C. AB + BC = AC                             
• D. Cả A, B, C đều sai

Câu 14: Cho tam giác ABC vuông tại A. Điểm E di động trên cạnh AB. Qua B vẽ một đường thẳng vuông góc với CE tại D và cắt tia CA tại H. Biết Cho tam giác ABC vuông tại A. Điểm E di động trên cạnh AB. Qua B vẽ một đường thẳng vuông góc với CE tại D và cắt tia CA tại H. Biết là: là:

• A. 30^o         

• B. 150^o       
• C. 60^o          
• D. 90^o

Câu 15: Cho đường tròn (O; R) và một điểm M nằm ở ngoài đường tròn sao cho MO = 2R. Đường thẳng d đi qua M, tiếp xúc với đường tròn (O; R) tại A. Giả sử N = MO ∩ (O; R). Kẻ hai đường kính AB, CD khác nhau của (O; R). Các đường thẳng BC, BD cắt đường thẳng d lần lượt tại P, Q. Khi đó:

• A. 3BQ – 2AQ > 4R                         

• B. 3BQ – 2AQ < 4R
• C. 3BQ – 2AQ = 4R                          
• D. A, B, C đều sai