BÀI 2. TỨ GIÁC NỘI TIẾP ĐƯỜNG TRÒN

Mở đầu: Hình 19 minh họa một đường tròn và tứ giác ABCD có bốn đỉnh thuộc đường tròn. Tứ giác ABCD được gọi là gì?

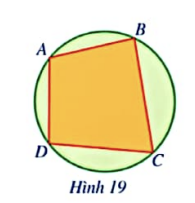
Đáp án chuẩn:

Tứ giác nội tiếp đường tròn

I. ĐỊNH NGHĨA

HĐ 1. Quan sát hình 20 và cho biết các đỉnh của tứ giác ABCD có thuộc đường tròn (O) hay không?

Đáp án chuẩn:

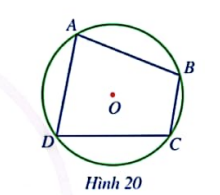
Các đỉnh của tứ giác ABCD có thuộc đường tròn (O).

Vận dụng 1. Dùng thước thẳng và compa vẽ một tứ giác nội tiếp đường tròn theo các bước sau:

-Vẽ một đường tròn;

-Vẽ tứ giác có bốn đỉnh thuộc đường tròn;

Đáp án chuẩn:

Bước 1: Dùng compa vẽ một đường tròn bất kì.

Bước 2: 1. Đánh dấu 4 điểm bất kì trên đường tròn.

              2. Nối các điểm đã đánh dấu theo thứ tự tạo thành một tứ giác.

II. TÍNH CHẤT

HĐ 2. Trong hình 22, cho biết . Tính số đo của các cung và góc sau theo

Đáp án chuẩn:

a) ;

b) =360ᵒ-α; =

180ᵒ

Vận dụng 2. Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC(M khác B và C). Tính số đo góc BMC.

Đáp án chuẩn:

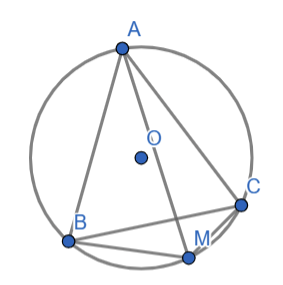
III. HÌNH CHỮ NHẬT,HÌNH VUÔNG NỘI TIẾP ĐƯỜNG TRÒN

HĐ 3. Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R=OA và vẽ đường tròn(O;R). Các điểm A,B,C,D có thuộc (O;R) hay không?

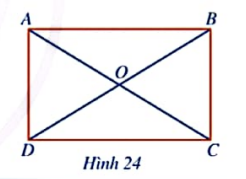
Đáp án chuẩn:

A,B,C,D thuộc đường tròn (O;R)

Vận dụng 3. Người ta làm một logo có dạng một hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8cm và 6cm. Hình chữ nhật được tô màu xanh còn phần khác của logo được tô màu đỏ. Tính diện tích phần được tô màu đỏ.

Đáp án chuẩn:

30,5cm

HĐ 4. Cho hình vuông ABCD, AC cắt BD tại điểm O (Hình 26).

a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?

b) Cho biết AB=a, tính OA theo a.

Đáp án chuẩn:

a) Mỗi đường chéo của hình vuông ABCD là đường kính của đường tròn ngoại tiếp hình vuông đó vì và AC=BD

b)

Vận dụng 4. Tính tỉ số giữa chu vi của một hình vuông và chu vi của đường tròn ngoại tiếp hình vuông đó

Đáp án chuẩn:

IV. GIẢI BÀI TẬP CUỐI SGK

Bài 1: Quan sát hình 28 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tứ giác ABCD, đường tròn nào ngoại tiếp tứ giác ABMN.

Đáp án chuẩn:

Đường tròn (O) ngoại tiếp tứ giác ABCD

Đường tròn (I) ngoại tiếp tứ giác ABMN

Bài 2: Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong mỗi trường hợp sau:

a) và

b) và

c) và

d) và

Đáp án chuẩn:

;

 ;

;

Bài 3: Cho tam giác ABC nội tiếp đường tròn (O) thỏa mãn Giả sử D là điểm thuộc cung BC không chứa A. Tính số đo góc BDC.

Đáp án chuẩn:

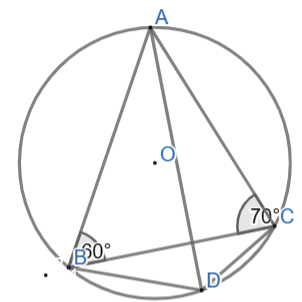
Bài 4: Mặt trên của tấm đệm có dạng hình tròn ở hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3dm, 5dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm (theo đơn vị dm vuông và làm tròn đến kết quả hàng trăm).

Đáp án chuẩn: 

26,68

Bài 5: Cho hình thang ABCD(AB//CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.

Đáp án chuẩn:

ABCD là hình thang cân

Bài 6: Cho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I.

a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao?

b) Chứng minh ΔIAB  ∼ ΔIDC và IA.IC=IB.ID

Đáp án chuẩn:

=

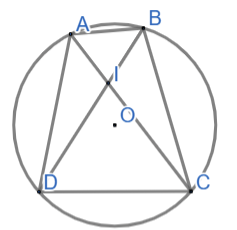
b) ΔIAB  ∼ ΔIDC (g.g) => IA.IC=IB.ID (đpcm)

Bài 7: Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM và CN của tam giác ABC cắt nhau tại H( hình 30). Chứng minh:

a)

Đáp án chuẩn:

a) MHNB là tứ giác nội tiếp

b);

(dpcm)

c) Có mà