BÀI 2. MỘT SỐ PHÉP TÍNH TÍNH VỀ CĂN BẬC HAI CỦA SỐ THỰC

Mở đầu: Khi một quả bóng rổ được thả xuống, nó sẽ nảy trở lại, nhưng do tiêu hao năng lượng nên nó không đạt được chiều cao như lúc ban đầu. Hệ số phục hồi của quả bóng rổ được tính theo công thức C_R = trong đó H là độ cao mà quả bóng được thả rơi và h là độ cao mà quả bóng bật lại.

(Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017)

Một quả bóng rổ rơi từ độ cao 3,24 m và bật lại độ cao 2,25 m. Làm thế nào để viết hệ số phục hồi của quả bóng đó dưới dạng phân số?

Đáp án chuẩn:

C_R = =

I. CĂN BẬC HAI CỦA MỘT BÌNH PHƯƠNG

HĐ 1. So sánh:

a)

b)

Đáp án chuẩn:

a)

b) .

Vận dụng 1. Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:

a)

b)

c) .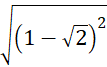

Đáp án chuẩn:

a) 35

b)

c)

II. CĂN BẬC HAI CỦA MỘT TÍCH

HĐ 2. So sánh:

Đáp án chuẩn:

Vận dụng 2. Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:

a)

b) ;

c) . 

Đáp án chuẩn:

a)

b)

c)

III. CĂN BẬC HAI CỦA MỘT THƯƠNG

HĐ 3. So sánh

Đáp án chuẩn:

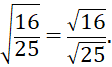
Vận dụng 3. Trong tình huống nêu ra ở phần mở đầu, hãy viết hệ số phục hồi của quả bóng rổ dưới dạng phân số.

Đáp án chuẩn:

C_R =

IV. ĐƯA THỪA SỐ RA NGOÀI DẤU CĂN BẬC HAI

HĐ 4. So sánh:

a)

b)

Đáp án chuẩn:

a)

b)

Vận dụng 4. Rút gọn biểu thức:

Đáp án chuẩn:

V. ĐƯA THỪA SỐ VÀO TRONG DẤU CĂN BẬC HAI

HĐ 5. So sánh:

a)

b)

Đáp án chuẩn:

a)

b)

Vận dụng 5. Rút gọn biểu thức:

a) ;

b) 6

Đáp án chuẩn:

a)

b) 6

VI. GIẢI BÀI TẬP CUỐI SGK

Bài 1: Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:

a)

b)

c)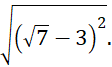

Đáp án chuẩn:

a) 25

b)

c)

Bài 2: Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:

a)

b)

c)

d)

Đáp án chuẩn:

a)

b)

c)

d)

Bài 3: Áp dụng quy tắc về căn bậc hai của một thương, hãy tính:

a)

b)

c)

d)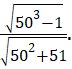

Đáp án chuẩn:

a)

b)

c)

d)

Bài 4: Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai, hãy rút gọn biểu thức:

a)

b)

c) .

Đáp án chuẩn: 

a)

b)

c)

Bài 5: Áp dụng quy tắc đưa thừa số vào trong dấu căn bậc hai, hãy rút gọn biểu thức:

a) ;

b) (

Đáp án chuẩn:

a)

b)

Bài 6: So sánh

a) ;

b)

c)

Đáp án chuẩn:

a)

b)

c)

Bài 7: Cho tam giác đều ABC có độ dài cạnh là a. Tính độ dài đường cao AH của tam giác ABC theo a.

Đáp án chuẩn:

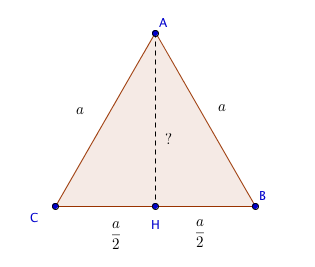
AH

Bài 8: Trong Vật lý, ta có định luật Joule – Lenz để tính nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua: Q =

Trong đó: Q là nhiệt lượng tỏa ra trên dây dẫn tính theo Joule (J);

I là cường độ dòng điện chạy trong dây dẫn tính theo Ampe (A);

R là điện trở dây dẫn tính theo Ohm (Ω);

t là thời gian dòng điện chạy qua dây dẫn tính theo giây.

Áp dụng công thức trên để giải bài toán sau: Một bếp điện khi hoạt động bình thường có điện trở R = 80 Ω. Tính cường độ dòng điện chạy trong dây dẫn, biết nhiệt lượng mà dây dẫn tỏa ra trong 1 giây là 500 J. 

Đáp án chuẩn:

2,5 A

Bài 9: Tốc độ gần đúng của một ô tô ngay trước khi đạp phanh được tính theo công thức v = trong đó v (m/s) là tốc độ của ô tô, d (m) là chiều dài của vết trượt tính từ thời điểm đạp phanh cho đến khi ô tô dừng lại trên đường, là hệ số cản lăn của mặt đường, g = 9,8 m/ (Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017). Nếu một chiếc ô tô để lại vết trượt dài 20 m trên đường nhựa thì tốc độ của ô tô trước khi đạp phanh là khoảng bao nhiêu đơn vị mét trên giây (làm tròn kết quả đến hàng đơn vị)? Biết rằng hệ số cản lăn cả đường nhựa đó là

Đáp án chuẩn:

17 m/s