BÀI 3. CĂN THỨC BẬC HAI VÀ CĂN THỨC BẬC BA CỦA BIỂU THỨC ĐẠI SỐ

Mở đầu: Để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn, người lái cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép v (m/s) được tính bởi công thức v = trong đó r (m) là bán kính của cung đường, g = 9,8 m/, là hệ số ma sát trượt của đường.

(Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017).

Hãy viết biểu thức tính v theo r khi biết Trong toán học, biểu thức đó được gọi là gì?

Đáp án chuẩn:

Biểu thức đại số

I. CĂN THỨC BẬC HAI

HĐ 1. Cửa hàng điện máy trưng bày một chiếc ti vi màn hình phẳng 55 in, tức là độ dài đường chéo của màn hình tivi bằng 55 in (1 in = 2,54 cm). Gọi x (in) là chiều rộng của màn hình tivi (Hình 5). Viết công thức tính chiều dài của màn hình tivi theo x.

Đáp án chuẩn:

Vận dụng 1. Mỗi biểu thức sau có phải là một căn thức bậc hai hay không?

a)

b) .

c)

Đáp án chuẩn:

a) Biểu thức là một căn thức bậc hai 

b) Biểu thức là một căn thức bậc hai 

c) Biểu thức không là một căn thức bậc hai

Vận dụng 2. Tính giá trị của tại:

a) x = 2; 

b) x =

Đáp án chuẩn:

a)

b)

HĐ 2. Cho căn thức bậc hai Biểu thức đó có xác định hay không tại mỗi giá trị sau?

a) x = 2.

b) x = 1

c) x = 0.

Đáp án chuẩn:

a) Biểu thức có xác định.

b) Biểu thức không xác định.

Vận dụng 3. Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a)  

b)

Đáp án chuẩn:

a)

b)

II. CĂN THỨC BẬC BA 

HĐ 3. Thể tích V của một khối lập phương được tính bởi công thức: V = với a là độ dài cạnh của khối lập phương. Viết công thức tính độ dài cạnh của một khối lập phương theo thể tích V của nó.

Đáp án chuẩn:

Vận dụng 4. Mỗi biểu thức sau có phải là một căn thức bậc ba hay không?

a) .

b)

c)

Đáp án chuẩn:

a) Biểu thức là một căn thức bậc ba 

b) Biểu thức là một căn thức bậc ba 

c) Biểu thức không là một căn thức bậc ba

Vận dụng 5. Tính giá trị của tại x = 3; x = – 2; x = – 10.

Đáp án chuẩn:

Thay x = 3, ta được:

Thay x = – 2, ta được

Thay x = – 10, ta được

HĐ 4. Cho căn thức bậc 3 Biểu thức đó có xác định hay không tại mỗi giá trị sau?

a) x = 17

b) x = 1.

Đáp án chuẩn:

a) Biểu thức có xác định.

b) Biểu thức không xác định.

Vận dụng 6. Tìm điều kiện xác định cho mỗi căn thức bậc ba sau:

a)

b)

Đáp án chuẩn:

a) mọi số thực x 

b)

III. GIẢI BÀI TẬP CUỐI SGK 

Bài 1: Tính giá trị của mỗi căn thức bậc hai sau:

a) tại x = 1; x = – 3; x = ;

b) tại x = 0; x = – 1; x = – 7.

Đáp án chuẩn:

a) Thay x = 1 ta được:

Thay x = – 3  ta được:

Thay x = – 7 ta được:. Biểu thức không xác định được. 

b) Thay x = 0 ta được:

Thay x = – 1 ta được: 

Thay x = – 7 ta được:

Bài 2: Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a)

b)

c)

Đáp án chuẩn:

a)

b)

c) x

Bài 3: Tính giá trị của mỗi căn thức bậc ba sau:

a) tại x = – 10; x = 7,5; x = – 0,5;

b) tại x = 0; x = 2; x =

Đáp án chuẩn: 

a) Thay x = – 10 ta được:

Thay x = 7,5 ta được:

Thay x = – 0,5 ta được:

b) Thay x = 0 ta được:

Thay x = 2 ta được:

Thay x = ta được:

Bài 4: Tìm điều kiện xác định cho mỗi căn thức bậc ba sau:

a)

b)

c)

 Đáp án chuẩn:

a) mọi số thực x.

b) mọi số thực x.

c) x

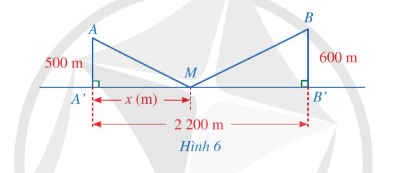
Bài 5: Có hai xã cùng ở một bên bờ sông. Người ta đo được khoảng cách từ trung tâm A, B của hai xã đó đến bờ sông lần lượt là AA’ = 500 m, BB’ = 600 m và khoảng cách A’B’ = 2 200 m (minh họa ở Hình 6). Các kỹ sư muốn xây một trạm cung cấp nước sạch nằm trên bờ sông cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sách đó là điểm M trên đoạn A’B’ với MA’ = x (m), 0 < x < 2 200.

a) Viết công thức tính tổng khoảng cách MA + MB theo x.

b) Tính tổng khoảng cách MA + MB khi x = 1 200 (làm tròn kết quả đến hàng đơn vị của mét).

Đáp án chuẩn:

a) 

b)

Bài 6: Hệ quả của hiện tượng nóng lên toàn cầu là băng của một số sông băng đang tan chảy. Mười hai năm sau khi băng biến mất, những loài thực vật nhỏ bé, được gọi là địa y, bắt đầu mọc trên đá. Mỗi nhóm địa y phát triển ở dạng (gần như) một hình tròn. Đường kính d (mm) của hình tròn này có thể được tính gần bằng công thức: 

d = với t là số năm tính từ khi băng biến mất (t(Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017).

Tính đường kính của hình tròn do địa y tạo nên sau khi băng biến mất 13 năm; 16 năm.

Đáp án chuẩn:

Đường kính của hình tròn sau khi băng biến mất 13 năm: (mm)

Đường kính của hình tròn sau khi băng biến mất 16 năm:

Bài 7: Chiều cao ngang vai của một con voi đực ở châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức: h = 62,5. + 75,8 với t là tuổi của co voi tính theo năm (Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017).

a) Một con voi đực 8 tuổi ở châu Phi sẽ có chiều cao ngang vai là bao nhiêu centimét?

b) Nếu một con voi đực ở châu Phi có chiều ngang vai là 205 cm thì con voi đó bao nhiêu tuổi (làm tròn kết quả đến hàng đơn vị)?

Giải chi tiết

a) 200,8 (cm)

b) 9 tuổi