Slide bài giảng Toán 11 cánh diều Chương 7 Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Tóm lược nội dung

CHƯƠNG 7: BÀI 1. ĐỊNH NGHĨA ĐẠO HÀM, Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM

I. ĐẠO HÀM TẠI MỘT ĐIỂM

Hoạt động 1: Tính vận tốc tức thời của viên bi tại thời điểm x_0=1(s) trong bài toán tìm vận tốc tức thời nêu ở trên.

Trả lời rút gọn:

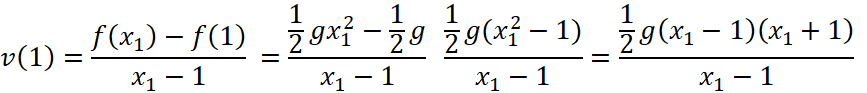
Luyện tập 1: Tính đạo hàm của hàm số ....

Trả lời rút gọn:

Xét là số gia của biến số tại điểm .

Vậy .

Luyện tập 2: Tính đạo hàm của hàm số f (x) = x³  tại điểm x bất kì bằng định nghĩa.

Trả lời rút gọn:

Xét là số gia của biến số tại điểm .

Vậy .

II. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM

Hoạt động 2: Cho hàm số y = f(x) có đồ thị (C) một điểm M₀ cố định thuộc (C) ...

a) Xác định hệ số góc k₀ của tiếp tuyến M₀T theo x₀.

b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M₀.

Trả lời rút gọn:

a)

b) Phương trình tiếp tuyến của đồ thị hàm số tại điểm

Luyện tập 3: Viết phương trình tiếp tuyến của đồ thị hàm số y = tại điểm N (1;1)

Trả lời rút gọn:

a) Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc là:

b) Phương trình tiếp tuyến của đồ thị tại điểm N (1; 1) là:

GIẢI BÀI TẬP CUỐI SGK

Bài 1. Tính đạo hàm của hàm số....

Trả lời rút gọn:

Xét là số gia của biến số tại điểm .

Ta có :

Vậy

Bài 2. Chứng minh rằng hàm số...

Trả lời rút gọn:

Xét là số gia của biến số tại điểm .

=> nên không tồn tại

Vậy hàm số không có đạo hàm tại điểm .

:

+ Với ta có hàm số .

Do đó thì hàm số có đạo hàm .

+ Với ta có hàm số .

Do đó thì hàm số có đạo hàm

Vậy hàm số không có đạo hàm tại điểm nhưng có đạo hàm tại mọi điểm .

Bài 3. Cho hàm số y = ....

Trả lời rút gọn:

a) Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 có hệ số góc là:

Vậy hệ số góc của tiếp tuyến của đồ thì (C) tại điểm có hoành độ bằng 2 là -7.

b) Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; -6) là :

Bài 4. Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là...

Trả lời rút gọn:

a) Xét là số gia của biến số tại điểm

=> .

Ta thấy

Vậy hàm chi phí biên là: (USD)

b)  (USD)

Ý nghĩa: Để sản xuất thêm 1 sản phẩm từ 90 lên 91 sản phẩm cần chi phí biên (chi phí gia tăng) là 260 (USD)