Slide bài giảng Toán 11 cánh diều Bài tập cuối chương 2

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG II

BT 1 trang 57 sgk toán 11 cánh diều

Cho dãy số (u_n) được xác định bởi: u₁ = 1/3 và u_n = 3u_n−1 với mọi n ≥ 2. Số hạng thứ năm của dãy số (_un) là:

A. 27

B. 9

C. 81

D. 243

Trả lời rút gọn:

A

 Do đó dãy só là một cấp số nhân với và q = 3 nên với .

BT 2 trang 57 sgk toán 11 cánh diều

Trong các dãy số (Un) có công thức của số hạng tổng quát Un sau đây, dãy số nào là dãy số tăng?

Trả lời rút gọn:

D

  với mọi

Vậy dãy số đã cho là dãy số tăng

BT 3 trang 57 sgk toán 11 cánh diều

Trong các dãy số sau, dãy số nào là cấp số cộng?

Trả lời rút gọn:

A

Dãy số 21; – 3; – 27; – 51; – 75 lập thành một cấp số cộng có số hạng đầu là và

BT 4 trang 57 sgk toán 11 cánh diều

Cho cấp số cộng (u_n) có số hạng đầu u₁ =  −5, công sai d = 4. Công thức của số hạng tổng quát u_n là:

A. u_n = −5 + 4n

B. u_n = − 1 − 4n

C. u_n = −5 + 4n²

D. u_n = −9 + 4n

Trả lời rút gọn:

D

BT 5 trang 57 sgk toán 11 cánh diều

Tổng 100 số tự nhiên lẻ đầu tiên tính từ 1 là:

A. 10 000

B. 10 100

C. 20 000

D. 20 200

Trả lời rút gọn:

A

Các số tự nhiên lẻ lập thành một cấp số cộng với và

BT 6 trang 57 sgk toán 11 cánh diều

Trong các dãy số (u_n) cho bằng phương pháp truy hồi sau, dãy số nào là cấp số nhân?

A. Dãy số (u_n) được xác định bởi: u₁ = 1 và u_n = u_n−1(n−1) với mọi n ≥ 2

B. Dãy số (u_n) được xác định bởi: u₁ = 1 và u_n = 2u_n−1+1 với mọi n ≥ 2

C. Dãy số (u_n) được xác định bởi: u₁ = 1 và u_n = u²_n−1 với mọi n ≥ 2

D. Dãy số (u_n) được xác định bởi: u₁ = 3 và u_n = 1/3u_n−1 với mọi n  ≥2

Trả lời rút gọn:

D

Dãy được xác định bởi: và với mọi là cấp số nhân với và

BT 7 trang 57 sgk toán 11 cánh diều

Cho cấp số nhân (u_n) có u₁ = −1, công bội q = −1/10. Khi đó 1/10²⁰¹⁷ là số hạng thứ: 

A. 2016

B. 2017

C. 2018

D. 2019

Trả lời rút gọn:

C

BT 8 trang 58 sgk toán 11 cánh diều

Xét tính tăng, giảm và bị chặn của mỗi dãy số (u_n) sau, biết số hạng tổng quát...

Trả lời rút gọn:

a) =>

(vì ).

Vậy nên là dãy số tăng.

+  

mà ().

Vậy dãy số bị chặn.

b) =>

nên là dãy số giảm.

+ . Vì (), mà ()

Vậy nên dãy số bị chặn

BT 9 trang 58 sgk toán 11 cánh diều

Cho cấp số cộng (u_n). Tìm số hạng đầu u₁, công sai d trong mỗi trường hợp sau:

a) u₂ + u₅ = 42 và u₄ + u₉ = 66

b) u₂ + u₄ = 22 và u₁.u₅ = 21

Trả lời rút gọn:

a)  

Khi đó ta có:

Vậy số hạng đầu của cấp số cộng là: và công sai
b)

Thay vào 

hoặc

Với thì .

Với thì .

BT 10 trang 58 sgk toán 11 cánh diều

Cho cấp số nhân (un).Tìm số hạng đầu u₁, công bội q trong mỗi trường hợp sau: 

a) u₆ = 192 và u₇ = 384

b) u₁ + u₂ + u₃ = 7 và u₅ − u₂ = 14

Trả lời rút gọn:

a) và

• q = 2

=>

Vậy cấp số nhân có số hạng đầu là và công bội

b)

Và

=> và  

Với thì

Với thì

BT 11 trang 58 sgk toán 11 cánh diều

Tứ giác ABCD có số đo bốn góc A, B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo góc C gấp 5 lần số đo góc A. Tính số đo các góc của tứ giác ABCD theo đơn vị độ.

Trả lời rút gọn:

Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:

B = A + d; C = A + 2d; D = A + 3d.

Mặt khác: A + B + C + D = 360°

⇔ A + A + d + A + 2d + A + 3d = 360°

⇔ 2A + 3d = 180°

Ta lại có: A + 2d = 5A ⇔ d = 2A

⇒ 8A = 180°

⇒ A = 22,5° và d = 45°

⇒ B = 67,5°, C = 112,5°, D = 157,5°.

BT 12 trang 58 sgk toán 11 cánh diều

Người ta trồng cây theo các hàng ngang với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây, ... ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4 950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?

Trả lời rút gọn:

Giải sữ người ta đã trồng được n hàng.

Số cây ở mỗi hàng lập thành một cấp số cộng với: , công sai

(TM) hoặc (KTM)

Vậy có 99 hàng cây được trồng theo cách trên.

BT 13 trang 58 sgk toán 11 cánh diều

Một cái tháp có 11 tầng. Diện tích của mặt sàn tầng 2 bằng nửa diện tích của mặt đáy tháp và diện tích của mặt sàn mỗi tầng bằng nửa diện tích của mặt sàn mỗi tầng ngay bên dưới. Biết mặt đáy tháp có diện tích là 12288 m². Tính diện tích của mặt sàn tầng trên cùng của tháp theo đơn vị mét vuông.

Trả lời rút gọn:

Diện tích mặt đáy tháp là

Diện tích mặt sàn tầng 2 là :

…

Gọi diện tích mặt sàn tầng n là với .

Dãy lập thành một cấp số nhân là và , có  .

BT 14 trang 58 sgk toán 11 cánh diều

Một khay nước có nhiệt độ 23^∘C được đặt vào ngăn đá của tủ lạnh. Biết sau mỗi giờ, nhiệt độ của nước giảm 20%. Tính nhiệt độ của khay nước đó sau 6 giờ theo đơn vị độ C.

Trả lời rút gọn:

Gọi u_n là nhiệt độ của khay nước đó sau n giờ (đơn vị độ C) với n ∈ ℕ*.

Suy ra dãy (u_n) lập thành một cấp số nhân với và c có độ C.

Vậy sau 6 giờ thì nhiệt độ của khay là .

BT 15 trang 58 sgk toán 11 cánh diều

Cho hình vuông C₁ có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C₂ (Hình 4). Từ hình vuông C₂ lại làm tiếp tục như trên để có hình vuông C₃. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông C₁,C₂,C₃,...,C_n,... Gọi a_n là độ dài cạnh hình vuông C_n. Chứng minh rằng dãy số (a_n) là cấp số nhân. 

Trả lời rút gọn:

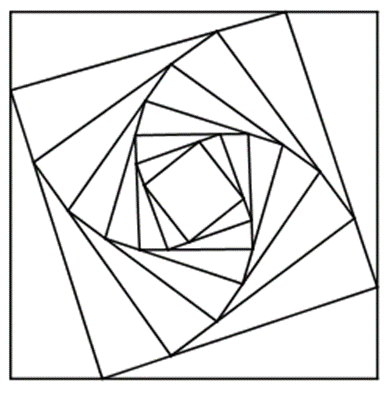
Độ dài cạnh của hình vuông đầu tiên là:

Độ dài cạnh của hình vuông thứ n là:

Độ dài cạnh của hình vuông thứ n + 1 là:

=>

Vậy (a_n) là một cấp số nhân với số hạng đầu và công bội .

BT 16 trang 58 sgk toán 11 cánh diều

Ông An vay ngân hàng 1 tỉ đồng với lãi suất 12%/năm. Ông đã trả nợ theo cách: Bắt đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là a (đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mỗi tháng mà ông An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?

Trả lời rút gọn:

Gọi u_n là số tiền sau mỗi tháng ông An còn nợ ngân hàng.

Lãi suất mỗi tháng là 1%.

đồng

(đồng)

…

+) Ta thấy dãy lập thành một cấp số nhân với và có tổng số hạng đầu là:

=>.

Vì sau thì ông An trả xong số tiền nên n = 24 và . 

. 

Vậy mỗi tháng ông An phải trả đồng.