Slide bài giảng Toán 11 cánh diều Chương 3 Bài 3: Hàm số liên tục

Tóm lược nội dung

BÀI 3. HÀM SỐ LIÊN TỤC 

I. KHÁI NIỆM

LT-VD 1 trang 74 sgk toán 11 cánh diều

Xét tính liên tục của hàm số f(x) = x³ + 1 tại x₀ = 1. 

Trả lời rút gọn:

và
=> .
Vậy hàm số liên tục tại

LT-VD 2 trang 75 sgk toán 11 cánh diều

Hàm số...có liên tục trên R hay không? 

Trả lời rút gọn:

+)  

và nên .

Suy ra hàm số không liên tục tại .

Vậy hàm số không liên tục trên .

II. MỘT SỐ ĐỊNH LÍ CƠ BẢN 

LT-VD 3 trang 76 sgk toán 11 cánh diều

Hàm số f(x)... có liên tục trên mỗi khoảng (−∞;8), (8;+∞) hay không?

Trả lời rút gọn:

  là hàm phân thức hữu tỉ xác định khi ; .

=>hàm số liên tục trên mỗi khoảng ; .

LT-VD 4 trang 76 sgk toán 11 cánh diều

Xét tính liên tục của hàm số f(x) = sinx + cosx trên R. 

Trả lời rút gọn:

Hàm số và liên tục trên .
=> liên tục trên .

BT 1 trang 77 sgk toán 11 cánh diều

Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x³ + x + 1 tại điểm x = 2 

Trả lời rút gọn:

xác định trên .

Do đó hàm số liên tục tại x = 2

BT 2 trang 77 sgk toán 11 cánh diều

Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích. 

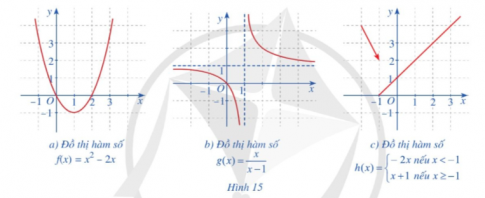
Trả lời rút gọn:

+) Hình 15a: Hàm số có .
Hàm số liên tục trên do đồ thị là đường cong liền.
+) Hình 15b: Hàm số có  .
Hàm số liên tục trên từng khoảng xác định của hàm số do đồ thị là đường cong liền trong các khoảng
+) Hình 15c:
Với có liên tục trên khoảng
Với có liên tục trên khoảng .
và

.
Do đó hàm số không liên tục tại .
Vậy hàm số liên tục trên các khoảng và .

BT 3 trang 77 sgk toán 11 cánh diều

Bạn Nam cho rằng: "Nếu hàm số y = f(x) liên tục tại điểm x₀, còn hàm số y = g(x) không liên tục tại x₀, thì hàm số y = f(x) + g(x) không liên tục tại x₀". Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích 

Trả lời rút gọn:

Hàm số liên tục tại điểm nên .
Hàm số không liên tục tại nên .
Do đó .
Vì vậy hàm số không liên tục tại .
Theo em ý kiến của bạn Nam là đúng

BT 4 trang 77 sgk toán 11 cánh diều

Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó...

Trả lời rút gọn:

a) Hàm số có D= .
Hàm số và liên tục trên nên hàm số liên tục trên .
b) Hàm số có D= .
Hàm số liên tục trên toàn bộ tập xác định
Hàm số liên tục trên các khoảng và .
Vậy hàm số đã cho liên tục trên từng khoảng xác định của hàm số.
c) Hàm số có .

Hàm số liên tục trên từng khoảng

BT 5 trang 77 sgk toán 11 cánh diều

Cho hàm số…

a) Với a = 0, xét tính liên tục của hàm số tại x = 4.

b) Với giá trị nào của a thì hàm số liên tục tại x = 4?

c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó? 

Trả lời rút gọn:

a) Với , tại , ta có:
và
=>
Vì vậy hàm số không liên tục tại .
b) Ta có: và
Để hàm số liên tục tại thì

Vậy với thì hàm số liên tục tại .

c) Hàm só có D=

Với có .

Hàm số liên tục trên các khoảng

Để hàm số liên tục trên thì hàm số phải liên tục tại .
Vậy với hàm số liên tục trên tập xác định của nó.

 

BT 6 trang 77 sgk toán 11 cánh diều

Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó h(t) = −2t² + 8t. 

a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định lim_t→2(−2t² + 8t).

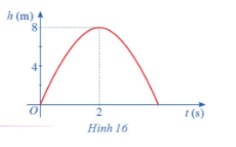
Trả lời rút gọn:

a) là hàm đa thức nên liên tục trên tập xác định.
b) Dựa vào đồ thị hàm số khi t tiến dần đến 2 thì h(t) dần đến 8 .
.