Slide bài giảng Toán 11 cánh diều Chương 6 Bài 3: Hàm số mũ. Hàm số lôgarit
Slide điện tử Chương 6 Bài 3: Hàm số mũ. Hàm số lôgarit. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3. HÀM SỐ MŨ. HÀM SỐ LÔGARIT
I. Hàm số mũ
Bài 1: Xét bài toán ở phần mở đầu.
a) Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm
b) Dự đoán công thức tính số tiền doanh nghiệp đó có được sau n năm
Trả lời rút gọn:
a) Số tiền doanh nghiệp đó có được:
+ Sau 1 năm: ![]() (đồng)
(đồng)
+ Sau 2 năm: ![]() (đồng)
(đồng)
+ Sau 3 năm: ![]() (đồng)
(đồng)
b)
![]()
Bài 2: Cho hai ví dụ về hàm số mũ
Trả lời rút gọn:
![]() ;
; ![]()
Bài 3: Cho hàm số mũ ![]() ...
...
Trả lời rút gọn:
a)
|
|
|
|
|
|
|
|
|
|
|
|
b)
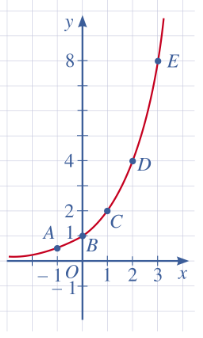
c) Tọa độ giao điểm của đồ thị ![]() với trục tung là
với trục tung là ![]()
Đồ thị không cắt trục hoành.
d) • ![]() ;
; ![]()
• Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
Bài 4: Cho hàm số mũ ![]() ...
...
Trả lời rút gọn:
a)
|
|
|
|
|
|
|
|
|
|
|
|
b)
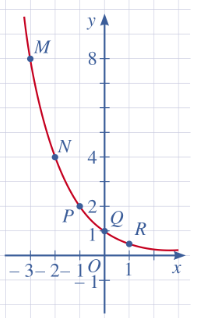
c) Tọa độ giao điểm của đồ thị hàm số ![]() với trục tung là
với trục tung là ![]()
Đồ thị hàm số ![]() không cắt trục hoành.
không cắt trục hoành.
d) ![]() ;
; ![]()
Hàm số ![]() nghịch biến trên
nghịch biến trên ![]() .
.

Bài 5: Lập bảng biến thiên và vẽ đồ thị hàm số ![]()
Trả lời rút gọn:
- ![]() là hàm số nghịch biến trên
là hàm số nghịch biến trên ![]() .
.
- Vì ![]() có cơ số
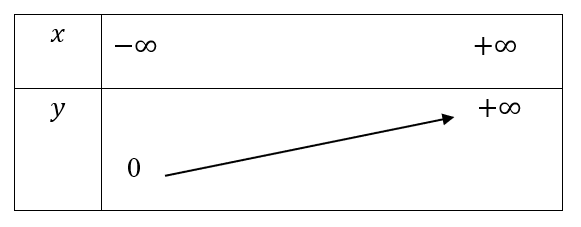
có cơ số ![]() nên ta có bảng biến thiên sau:
nên ta có bảng biến thiên sau:

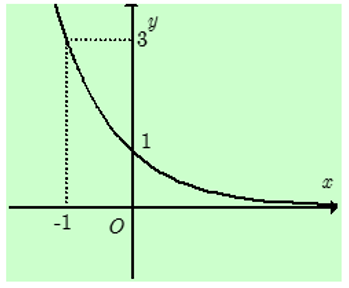
Đồ thị hàm số ![]() đi qua các điểm
đi qua các điểm ![]()
![]()
![]()
![]()
![]()
II. Hàm số lôgarit
Bài 1: Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
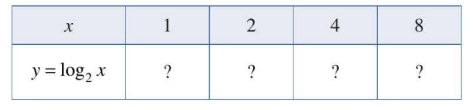
Trả lời rút gọn:
|
| 2 | 4 | 8 |
|
|
|
|
|
Bài 2: Cho hai ví dụ về hàm số lôgarit
Trả lời rút gọn:
![]() ;
; ![]()
Bài 3: Cho hàm số lôgarit ![]() ...
...
Trả lời rút gọn:
a)
|
|
|
|
|
|
|
|
|
|
|
|
b)
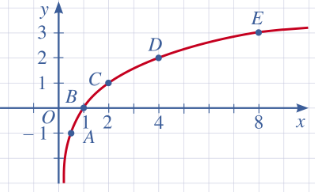
c) Tọa độ giao điểm của đồ thị hàm số ![]() với trục hoành là
với trục hoành là ![]()
Đồ thị hàm số đó không cắt trục tung.
d) ![]() ;
; ![]()
Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
Bài 4: Cho hàm số lôgarit ![]() ...
...
Trả lời rút gọn:
a)
|
|
|
|
|
|
|
|
|
|
|
|
b)
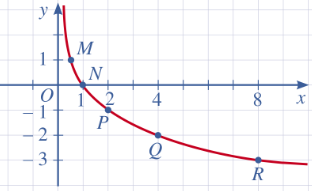
c) Tọa độ giao điểm của đồ thị hàm số ![]() với trục hoành là
với trục hoành là ![]()
+ Đồ thị hàm số không cắt trục tung.
d) ![]() ;
; ![]()
Hàm số ![]() nghịch biến trên
nghịch biến trên ![]() .
.
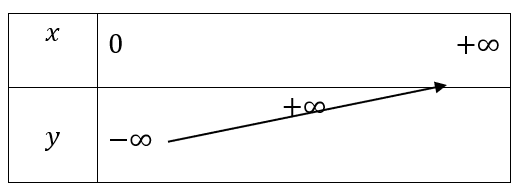
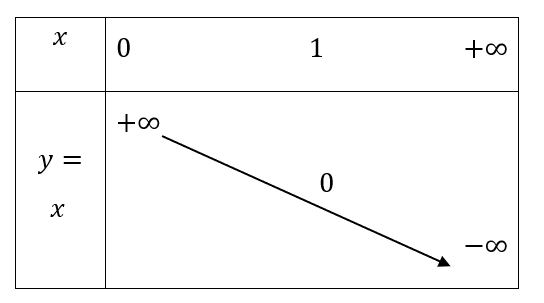
Bài 5: Lập bảng biến thiên và vẽ đồ thị hàm số ![]()
Trả lời rút gọn:
Vì hàm số ![]() có cơ số
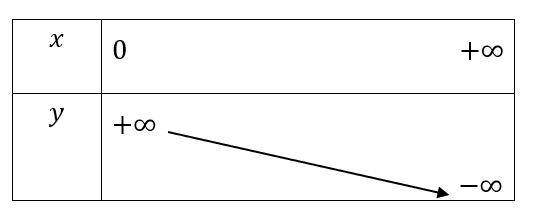
có cơ số ![]() nên ta có bảng biến thiên như sau:
nên ta có bảng biến thiên như sau:
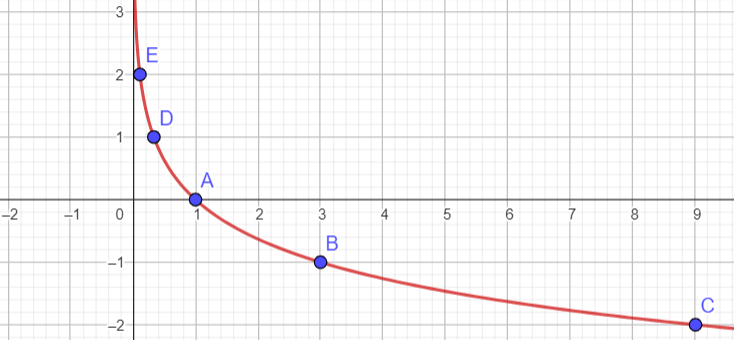
Đồ thị của hàm số ![]() là một đường cong liền nét đi qua các điểm
là một đường cong liền nét đi qua các điểm ![]()
![]()
III. Bài tập
Bài 1: Tìm tập xác định của các hàm số…
Trả lời rút gọn: a) |
b) |
c) |
Bài 2: Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?...
Trả lời rút gọn:
a) ![]()
Hàm số nghịch biến trên ![]() . Vì
. Vì ![]()
b) ![]()
Hàm số nghịch biến trên ![]() . Vì
. Vì ![]()
c) ![]()
Hàm số đồng biến trên ![]() . Vì
. Vì ![]()
d) ![]()
Hàm số nghịch biến trên ![]() . Vì
. Vì ![]()
