Slide bài giảng Toán 11 cánh diều Chương 4 Bài 3: Đường thẳng và mặt phẳng song song

Tóm lược nội dung

BÀI 3. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

I. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG   

LT-VD 1 trang 102 sgk toán 11 cánh diều

Quan sát các xà ngang trên sân tập thể dục ở Hình 47. Hãy cho biết vị trí tương đối của các xà ngang đó với mặt sân. 

Trả lời rút gọn:

Vị trí tương đối của xà ngang với mặt sàn là đường thẳng song song với mặt phẳng.

II. ĐIỀU KIỆN VÀ TÍNH CHẤT 

LT-VD 2 trang 102 sgk toán 11 cánh diều 

Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao? 

Trả lời rút gọn:

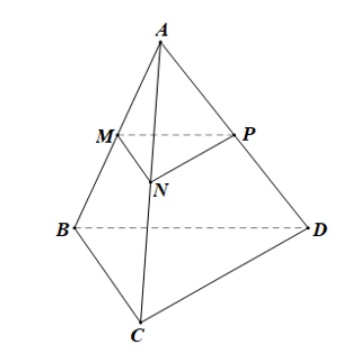
Xét có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác

=>MN // BC

Lại có  

=>MN // (BCD).

+) Chứng minh tương tự: NP // CD, CD ⊂ (BCD)

=>NP // (BCD).

+) Tương tự, MP // BD mà BD ⊂ (BCD) .

=>MP // (BCD).

LT-VD 3 trang 103 sgk toán 11 cánh diều

Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD). 

Trả lời rút gọn:

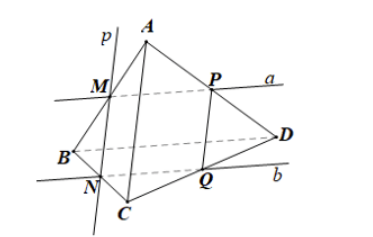
+) (R) đi qua M và // BD, mà BD ⊂ (ABD) 

=>(R) cắt (ABD) theo giao tuyến a đi qua M và // BD.

+) Gọi N là giao điểm của p và BC. Khi đó N ∈ (R).

(R) đi qua N và // BD, mà BD ⊂ (BCD)

=>(R) cắt (BCD) theo giao tuyến b đi qua N và // BD.

+) Gọi P là giao điểm của a và AD, Q là giao điểm của b và CD.

P ∈ (R) và P ∈ (ACD) nên P là giao điểm của (R) và (ACD);

Q ∈ (R) và Q ∈ (ACD) nên Q là giao điểm của (R) và (ACD).

=>PQ là giao tuyến của (R ) và (ACD).

LT-VD 4 trang 103 sgk toán 11 cánh diều

Trong Hình 56, hai mặt tường của căn phòng gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến b, mép cột gợi nên hình ảnh đường thẳng a. Cho biết đường thẳng a có song song với giao tuyến b hay không.

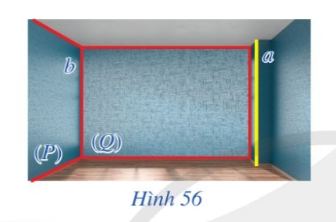
Trả lời rút gọn:

a // (P); a // (Q); (P) ∩ (Q) = b.

Do đó theo hệ quả định lí 2 ta có a // b.

BT 1 trang 103 sgk toán 11 cánh diều

Trong phòng học của lớp, hãy nêu những hình ảnh về đường thẳng song song với mặt phẳng. 

Trả lời rút gọn:

Những hình ảnh về đường thẳng song song với mặt phẳng: đường chân tường và trần nhà; mép tường và bức tường; …

BT 2 trang 103 sgk toán 11 cánh diều

Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.

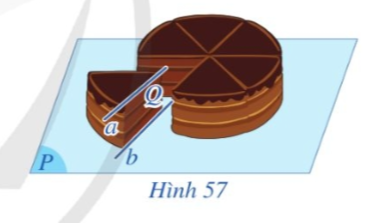
Trả lời rút gọn:

a // (P); a ⊂ (Q); (P) ∩ (Q) = b.    

Do đó theo định lí 2, a // b.

BT 3 trang 103 sgk toán 11 cánh diều

Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).

Trả lời rút gọn:

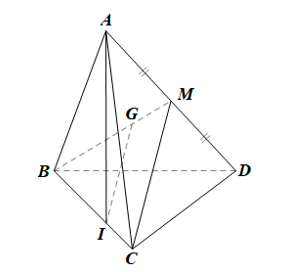
Gọi M là trung điểm của AD.

+)  Xét có G là trọng tâm tam giác nên

BI = 2IC nên

=> IG // CM 

+) IG // CM; CM ⊂ (ACD)

=> IG // (ACD).

BT 4 trang 103 sgk toán 11 cánh diều

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD). 

Trả lời rút gọn:

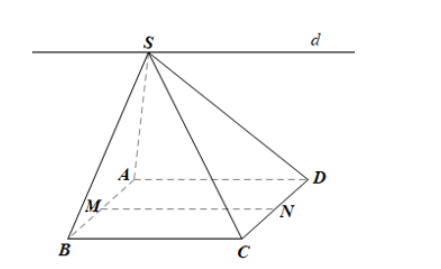
+) S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).

AD // BC (do ABCD là hình bình hành); AD ⊂ (SAD); BC ⊂ (SBC).

=> giao tuyến d của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.

+) Vì M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình

=> MN // BC // AD.

=> MN // d.

BT 5 trang 103 sgk toán 11 cánh diều

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF). 

Trả lời rút gọn:

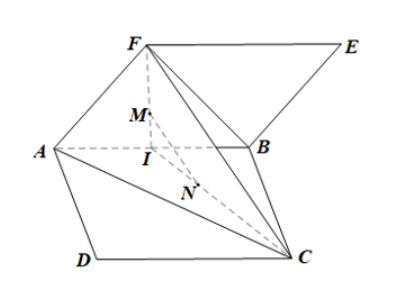
Gọi I là trung điểm của AB.

M là trọng tâm của tam giác nên

N là trọng tâm của tam giác nên

=> MN // FC (theo định lí Thalès)

Mà FC ⊂ (ACF).

=> MN // (ACF).

BT 6 trang 103 sgk toán 11 cánh diều

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho AD = 3AM. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC. 

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD). 

b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).

Trả lời rút gọn:

a)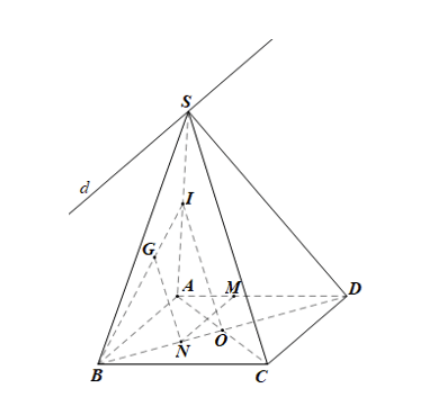

 S ∈ (SAB) và S ∈ (SCD) nên S là giao điểm của (SAB) và (SCD).

AB // CD (do ABCD là hình bình hành); AB ⊂ (SAB); CD ⊂ (SCD).

=> giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d đi qua S và song song với AB, CD.

b) 

+) Gọi O là tâm của hình bình hành, khi đó

N là trọng tâm của nên =>

nên

=> MN//AB.

+) Trong mặt phẳng (ABCD) có: AB // CD và MN // AB nên MN // CD.

Lại có CD ⊂ (SCD)

=>MN // (SCD).

+) Gọi I là trung điểm của SA.

Xét có G là trọng tâm của tam giác nên

=> GN // IO (theo định lí Thalès đảo)

Mà IO ⊂ (SAC) nên GN // (SAC).