Slide bài giảng Toán 11 cánh diều Chương 4 Bài 1: Đường thẳng và mặt phẳng trong không gian

Tóm lược nội dung

CHƯƠNG IV. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG

BÀI 1: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN 

I. KHÁI NIỆM MỞ ĐẦU

LT-VD 1 trang 86 sgk toán 11 cánh diều

Nêu ví dụ trong thực tiễn minh họa hình ảnh của một phần mặt phẳng. 

Trả lời rút gọn:

Các ví dụ về một phần của mặt phẳng là: Mặt bàn, mặt ghế, nền nhà, …

LT-VD 2 trang 87 sgk toán 11 cánh diều   

Vẽ hình biểu diễn của mặt phẳng (P) và đường thẳng a xuyên qua nó. 

Trả lời rút gọn:

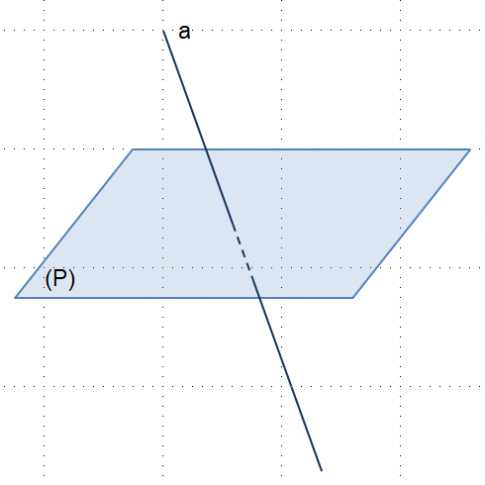
II. CÁC TÍNH CHẤT THỪA NHẬN CỦA HÌNH HỌC KHÔNG GIAN

LT-VD 3 trang 89 sgk toán 11 cánh diều

Trong Ví dụ 4, xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).

Trả lời rút gọn:

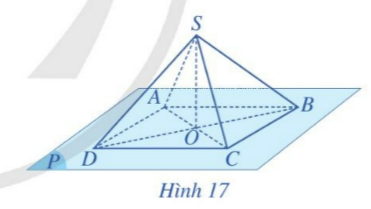
AC cắt BD tại O nên O thuộc hai mặt phẳng (SAC) và (SBD).

Mà S cũng thuộc hai mặt phẳng (SAC) và (SBD). 

=> SO là giao tuyến của hai mặt phẳng.

III. MỘT SỐ CÁCH XÁC ĐỊNH MẶT PHẲNG

LT-VD 4 trang 90 sgk toán 11 cánh diều

Trong mặt phẳng (P) cho tam giác ABC. Điểm D không thuộc mặt phẳng (P). Hỏi qua hai đường thẳng AD và BC có xác định được một mặt phẳng không? Trả lời rút gọn:

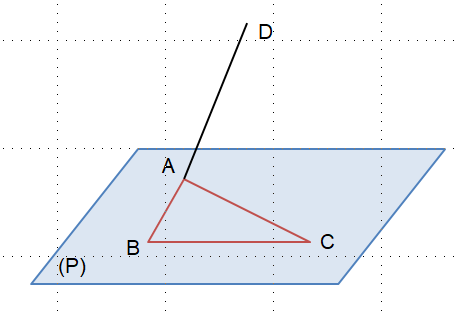
Giả sử có mặt phẳng đi chứa hai đường thẳng AD và BC.

Khi đó

Mà

mặt phẳng trùng mặt phẳng (P), nhưng điểm D không thuộc (P).

=>mâu thuẫn.

Vậy AD và BC không xác định được một mặt phẳng.

IV. HÌNH CHÓP VÀ HÌNH TỨ DIỆN

LT-VD 5 trang 92 sgk toán 11 cánh diều

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.

a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB. 

b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC).

Trả lời rút gọn:

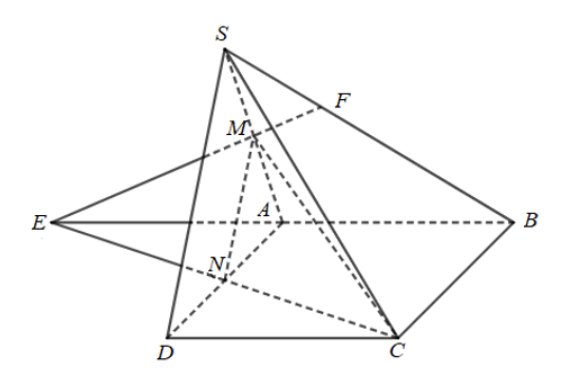
+) Trong mặt phẳng (ABCD): Gọi giao điểm của AB với NC là E.

Mà

=>E là giao điểm của AB và (CMN).

+) Trong mặt phẳng (SAB): Kéo dài EM cắt SB tại F. Mà

=>F là giao điểm của SB và (CMN).

b)

+) mà

mà nên

=>M là giao điểm của hai mặt phẳng (SAB) và (CMN).

=> E là giao điểm của hai mặt phẳng (SAB) và (CMN).

Vì vậy EM là giao tuyến của (SAB) và (CMN).

+) Ta có:

=>C là giao điểm của hai mặt phẳng (SBC) và (CMN).

=> F là giao điểm của hai mặt phẳng (SBC) và (CMN).

Vì vậy CF là giao tuyến của hai mặt phẳng (SBC) và (CMN).

LT-VD 6 trang 93 sgk toán 11 cánh diều

Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho...

a) Xác định E, F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP).

b) Chứng minh rằng các đường thẳng NE, PF và CD cùng đi qua một điểm.

Trả lời rút gọn:

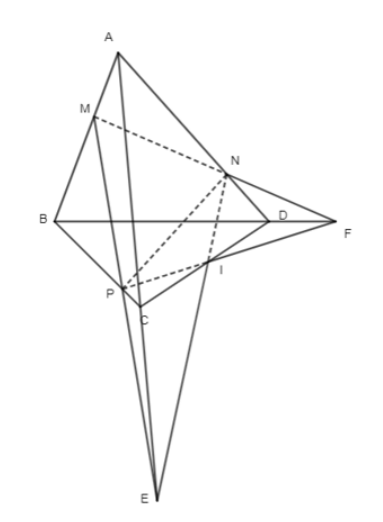
a)

+) Trong mặt phẳng (ABC), gọi giao điểm của MP  với AC là E.

Mà MP ⊂ (MNP) nên E là giao điểm của AC với (MNP).

+) Trong mặt phẳng (ABD), gọi giao điểm của MN với BD là F.

Mà MN ⊂ (MNP) nên F là giao điểm của BD với (MNP).

b) 

Trong mặt phẳng (ACD), nối NE cắt CD tại I.

 và

Khi đó I thuộc giao tuyến của (MNP) và (BCD).

Mà PF là giao tuyến của (MNP) và (BCD).

=>PF đi qua I.

Vậy các đường thẳng NE, PF và CD cùng đi qua một điểm.

BT 1 trang 94 sgk toán 11 cánh diều

Khi trát tường, dụng cụ không thể thiếu của người thợ là thước dẹt dài (Hình 28). Công dụng của thước dẹt này là gì? Giải thích. 

Trả lời rút gọn:

Công dụng: Kiểm tra xem mặt tường đã phẳng chưa.

Áp thước vào mặt tường, nếu thước đó luôn áp sát mặt tường (không bị cập kênh) thì mặt sàn là phẳng.

BT 2 trang 94 sgk toán 11 cánh diều

Hình 29 là hình ảnh của chặn giấy bằng gỗ có bốn mặt phân biệt là các tam giác. Vẽ hình biểu diễn của chặn giấy bằng gỗ đó. 

Trả lời rút gọn:

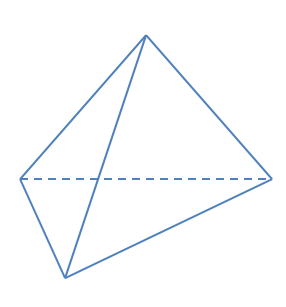
BT 3 trang 94 sgk toán 11 cánh diều

Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy. 

Trả lời rút gọn:

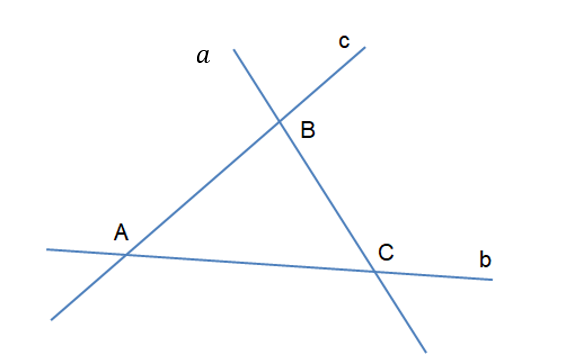
Giả sử: Sao cho: A, B, C không đồng quy (1)

B và C thuộc đường thẳng

Mà: =>

Do đó:

Nên ba đường thẳng đồng phẳng. Trái với giả thiết ba đường thẳng không cùng nằm trong mặt phẳng.

=>Ba điểm A, B, C phải trùng nhau; hay đồng quy.

BT 4 trang 94 sgk toán 11 cánh diều

Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng. 

Trả lời rút gọn:

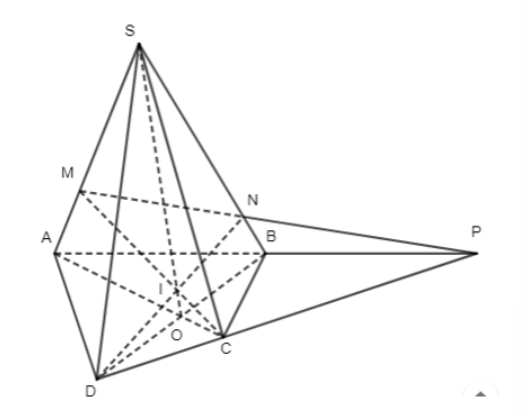
+) S ∈ (SAC) và S ∈ (SBD)

Mặt khác: AC ∩ BD = {O}; AC ⊂ (SAC); BD ⊂ (SBD).

Do đó O là giao điểm của (SAC) và (SBD).

=> SO là giao tuyến của (SAC) và (SBD).

+) Trong mặt phẳng (DMNC) có:

 DN ∩ MC = {I}; DN ⊂ (SDB); MC ⊂ (SAB).

Do đó I là giao điểm của (SAC) và (SBD).

=>SO đi qua điểm I.

Vậy S, I, O thẳng hàng.

BT 5 trang 94 sgk toán 11 cánh diều

Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho MA= 2MS, NS = 2NC. 

a) Xác định giao điểm của MN với mặt phẳng (ABC).

b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC).

Trả lời rút gọn:

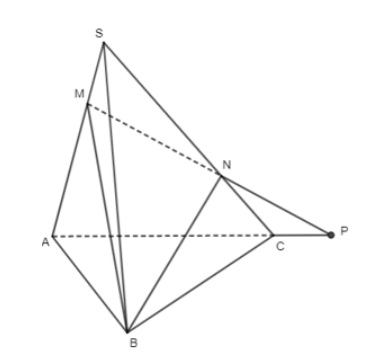
a) Trong mặt phẳng (SAC), gọi giao điểm của MN và AC là P.

=> P là giao điểm của MN và (ABC). 

b) MN ∩ (ABC) = {P} nên P ∈ (ABC)

P ∈ MN mà MN ⊂ (BMN) nên P ∈ (BMN)

=>P là giao điểm của (BMN) và (ABC).

B ∈ (BMN) và B ∈ (ABC).

=>B là giao điểm của (BMN) và (ABC).

Vì vậy BP là giao tuyến của (BMN) và (ABC).

BT 6 trang 94 sgk toán 11 cánh diều

Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA. 

a) Xác định giao điểm của CD với mặt phẳng (SAB). 

b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC).

Trả lời rút gọn:

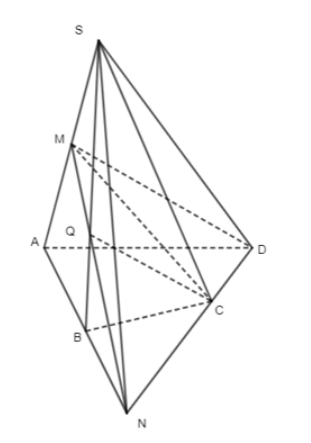
a) Trong mặt phẳng (ABCD): gọi giao điểm của AB và CD là N.

Mà AB ⊂ (SAB)

Do đó N là giao điểm CD và (SAB).

b) AB ∩ CD = {N}; AB ⊂ (SAB); CD ⊂ (SCD)

Do đó N thuộc (SAB) và (SCD).

S ∈ (SAB) và S ∈ (SCD)..

=>SN là giao tuyến của (SAB) và (SCD)

c)C ∈ (SBC) và C ∈ (MCD).

=>C là giao điểm của (SBC) và (MCD).

Trong mặt phẳng (SAB), gọi Q là giao điểm của MN và SB.

Mà MN ⊂ (MCD) và SB ⊂ (SBC)  

=>CQ là giao tuyến của (SBC) và (MCD).

BT 7 trang 94 sgk toán 11 cánh diều

Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA. 

a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).

b) Gọi G là giao điểm của AM và BN. Chứng minh rằng…

c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và…

Trả lời rút gọn:

a)

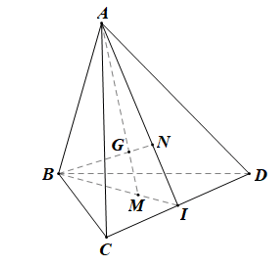
+) Xét tam giác BCD có: I là trung điểm của CD nên BI là đường trung tuyến.

Mà M là trọng tâm tam giác BCD nên BI đi qua M.

=>M ∈ BI.

BI ⊂ (ABI) nên M ∈ (ABI).

+) Xét tam giác ACD có: I là trung điểm của CD nên AI là đường trung tuyến.

Mà N là trọng tâm tam giác ACD nên AI đi qua N.

=>N ∈ AI.

AI ⊂ (ABI) nên N ∈ (ABI).

b) Trong có M là trọng tâm nên .

Trong có N là trọng tâm nên

Xét có  nên MN // AB (theo định lí Thalès đảo).

MN // AB

=> 

MN // AB

=>

Vậy

c)

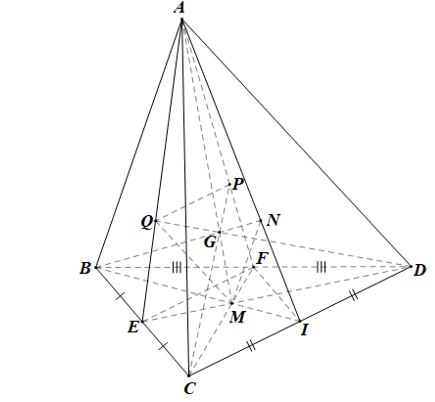
+) Gọi G’ là giao điểm của AM và CP; G’’ là giao điểm của AM và DQ.

Chứng minh tương tự câu b, ta có: 

(do PM//AC).

(do QM//AD)

=> , mà G, G’, G’’ cùng nằm trên AM nên ba điểm đó trùng nhau.

Vậy các đường thẳng CP, DQ cùng đi qua điểm G.

+) Xét tam giác ABC, kẻ đường trung tuyến AE (E ∈ BC).

Q là trọng tâm nên

Xét tam giác ABD, kẻ đường trung tuyến AF (F ∈ BD).

P là trọng tâm  nên

nên PQ//EF.

Mà EF // CD (đường trung bình tam giác BCD).

=> PQ // CD

Theo hệ quả định lí Thalès: .