Slide bài giảng Toán 11 cánh diều Chương 3 Bài 1: Giới hạn của dãy số

Tóm lược nội dung

CHƯƠNG III: GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 1: GIỚI HẠN CỦA DÃY SỐ

I. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

LT-VD 1 trang 60 sgk toán 11 cánh diều

Chứng minh rằng...

Trả lời rút gọn:

a)  với mọi

Với mọi h > 0 => với mọi

Vậy lim 0 = 0.

b)  với mọi

Với mọi bé tùy ý

Vậy với n > thì

Theo định nghĩa, ta có .

LT-VD 2 trang 61 sgk toán 11 cánh diều

Chứng minh rằng lim...

Trả lời rút gọn:

Đặt

Do

Vậy

LT-VD 3 trang 62 sgk toán 11 cánh diều

Chứng minh rằng lim...

Trả lời rút gọn:

0< do đó

II. ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN

LT-VD 4 trang 62 sgk toán 11 cánh diều

Tính các giới hạn sau...

Trả lời rút gọn:

a)

b)

III. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN 

LT-VD 5 trang 63 sgk toán 11 cánh diều

Tính tổng...

Trả lời rút gọn:

là một cấp số nhân lùi vô hạn với số hạng đầu và  

Nên

LT-VD 6 trang 63 sgk toán 11 cánh diều

Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng...

Trả lời rút gọn:

Thời gian Achilles chạy hết các quãng đường có độ dài 100 km, 1 km, km, km,... lần lượt là 1h, ,

Vậy Archilles đuổi kịp rùa sau giờ.

IV. GIỚI HẠN VÔ CỰC

LT-VD 7 trang 64 sgk toán 11 cánh diều

Tính lim ( - n³)

Trả lời rút gọn:

Với M là số dương bất kì, ta thấy

=> thì . 

=>

LT-VD 8 trang 64 sgk toán 11 cánh diều

Chứng tỏ rằng lim...

Trả lời rút gọn:

BT 1 trang 64 sgk toán 11 cánh diều

Cho hai dãy số (u_n), (v_n) với u_n = 3 + 1/n; v_n = 5 – 2/n². Tính các giới hạn sau:

a) lim u_n, lim v_n.

b) lim (u_n + v_n), lim (u_n − v_n), lim (u_n.v_n), lim u_n/v_n

Trả lời rút gọn:

a)

b)

BT 2 trang 65 sgk toán 11 cánh diều

Tính các giới hạn sau…

Trả lời rút gọn:

a)

b)

c) .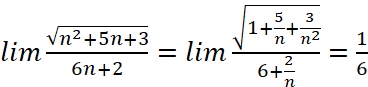
d) .
e) .
g)

 

BT 3 trang 65 sgk toán 11 cánh diều

a) Tính tổng của cấp số nhân lùi vô hạn (u_n), với (u_n), với u₁ = 2/3,q = −1/4.

b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số. 

Trả lời rút gọn:

a)với là:

b)

Dãy số 0,... lập thành một cấp số nhân có số hạng đầu và công bội có nên ta có:

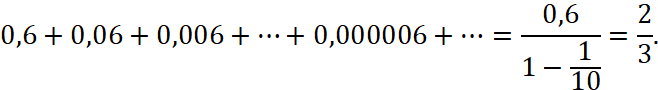
Suy ra .

 

BT 4 trang 65 sgk toán 11 cánh diều

Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn. 

a) Tính diện tích Sn của hình vuông được tạo thành ở bước thứ n;

b) Tính tổng diện tích của tất cả các hình vuông được tạo thành. 

Trả lời rút gọn:

a) Gọi là diện tích của hình vuông ban đầu cạnh bằng 1.

Gọi là diện tích của hình vuông tạo thành ở bước thứ , có cạnh bằng nên diện tích là

là diện tích của hình vuông tạo thành ở bước thứ , có cạnh bằng nên diện tích là
Dãy lập thành cấp số nhân có số hạng đầu và công bội có công thức tổng quát là:
b)  nên dãy trên lập thành một cấp số nhân lùi hạn.

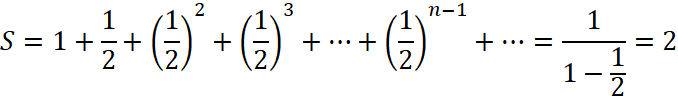
Vậy tổng diện tích của các hình vuông là 2 (đvdt).  

BT 5 trang 65 sgk toán 11 cánh diều

Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T= 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã). (Nguồn: Đại số và Giải tích 11, NXBGD Việt Nam, 2021)

Gọi u_n là khối lượng chất phóng xạ còn lại sau chu kì thứ n. 

a) Tìm số hạng tổng quát u_n của dãy số (u_n).

b) Chứng minh rằng (u_n) có giới hạn là 0.

c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10⁻⁶ g. 

Trả lời rút gọn:

a) Sau 1 chu kì ban rã thì (kg)

Sau 2 chu kì bán rã thì (kg),…

Sau n chu kì bán rã, khối lượng chất phóng xạ còn lại là: .
b)  .
c) Đổi
Vì chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn nên ta có

.

Vậy cần ít nhất 30 chu kì tương ứng với 720 000 năm khối lượng chất phóng xạ đã cho ban đầu không còn độc hại với con người.

BT 6 trang 65 sgk toán 11 cánh diều

Gọi C là nửa đường tròn đường kính AB = 2R, C₁  là đường gồm hai nửa đường tròn đường kính AB/2, C₂ là đường gồm bốn nửa đường tròn đường kính AB/4, Cn là đường gồm 2ⁿ nửa đường tròn đường kính AB/2ⁿ,... (Hình 4). Gọi p_n là độ dài của C_n, S_n là diện tích hình phẳng giới hạn bởi C_n và đoạn thẳng AB. 

a) Tính p_n, S_n. 

b) Tìm giới hạn của các dãy số (p_n) và (S_n)

Trả lời rút gọn:

a)

+) Một nửa đường tròn của có bán kính là
+)
+)

b)