Slide bài giảng Toán 11 cánh diều Chương 3 Bài 2: Giới hạn của hàm số

Tóm lược nội dung

BÀI 2: GIỚI HẠN CỦA HÀM SỐ

I. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM

LT-VD 1 trang 67 sgk toán 11 cánh diều

Sử dụng định nghĩa, chứng minh rằng lim_x→2 x² = 4. 

Trả lời rút gọn:

 
Giả sử là dãy số thỏa mãn .
.
=> .

LT-VD 2 trang 68 sgk toán 11 cánh diều

Tính...

Trả lời rút gọn:

a) .
b) .

LT-VD 3 trang 69 sgk toán 11 cánh diều

Tính...

Trả lời rút gọn:

II. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC

LT-VD 4 trang 70 sgk toán 11 cánh diều

Tính lim_{x→−∞...}

Trả lời rút gọn:

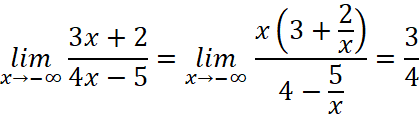
III. GIỚI HẠN VÔ CỰC (MỘT PHÍA) CỦA HÀM SỐ TẠI MỘT ĐIỂM

LT-VD 5 trang 71 sgk toán 11 cánh diều

Tính: lim_x→−2...

Trả lời rút gọn:

IV. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI VÔ CỰC

LT-VD 6 trang 72 sgk toán 11 cánh diều

Tính: lim_x→−∞x⁴

Trả lời rút gọn:

BT 1 trang 72 sgk toán 11 cánh diều

Sử dụng định nghĩa, tìm các giới hạn sau…

Trả lời rút gọn:

a) 
Giả sử là dãy số thỏa mãn .
.
=> .
b) 
Giả sử là dãy số thỏa mãn .
.
=>

BT 2 trang 72 sgk toán 11 cánh diều

Biết rằng hàm số f(x) thỏa mãn lim_x→2−f(x) = 3 và lim_x→2+f(x) = 5. Trong trường hợp này có tồn tại giới hạn lim_x→2f(x) hay không? Giải thích. 

Trả lời rút gọn:

  và  

=> nên không tồn tại .

BT 3 trang 72 sgk toán 11 cánh diều

Tính các giới hạn sau…

Trả lời rút gọn:

a)
b) .
c)

BT 4 trang 72 sgk toán 11 cánh diều

Tính các giới hạn sau…

Đáp án:

a) .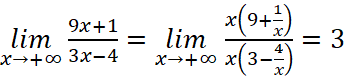
b) .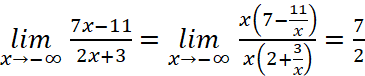
c) .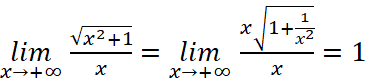
d) .
e)
g)

BT 5 trang 72 sgk toán 11 cánh diều

Một công ty sản xuất máy tính đã xác định được rằng, trung bình một nhân viên có thể lắp ráp được N(t)=50t/(t+4) (t≥0) bộ phận mỗi ngày sau t ngày đào tạo. Tính lim_t→+∞N(t) và cho biết ý nghĩa của kết quả. 

Trả lời rút gọn:

.
Ý nghĩa: Khi thời gian càng lớn thì số bộ phận mỗi ngày một nhân viên làm được càng gần 50 bộ phận

BT 6 trang 72 sgk toán 11 cánh diều

Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50000 + 105x...

Trả lời rút gọn:

a) Chi phí trung bình để sản xuất một sản phẩm là:
sản phẩm).
b) 

Ý nghĩa: Khi số sản phẩm càng lớn thì chi phí trung bình sản xuất một sản phẩm càng dần tới 105 nghìn đồng.