Slide bài giảng Toán 11 cánh diều Chương 4 Bài 5: Hình lăng trụ và hình hộp

Tóm lược nội dung

BÀI 5. HÌNH LĂNG TRỤ VÀ HÌNH HỘP

I. HÌNH LĂNG TRỤ 

LT-VD 1 trang 111 sgk toán 11 cánh diều

Cho một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ.

 Trả lời rút gọn:

Tháp Blade, lồng đèn, lều,…

II. HÌNH HỘP

LT-VD 2 trang 112 sgk toán 11 cánh diều 

Hãy liệt kê các đường chéo của hình hộp ABCD.A'B'C'D' (Hình 73). 

Trả lời rút gọn:

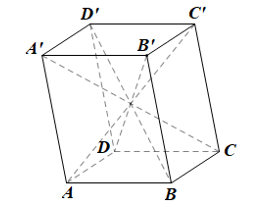
Các đường chéo của hình hộp là

LT-VD 3 trang 113 sgk toán 11 cánh diều

Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng bốn mặt phẳng (ABC'D'), (BCD'A'), (CDA'B'), (DAB'C') cùng đi qua một điểm. 

Trả lời rút gọn:

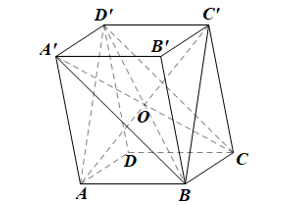
Gọi O là giao của AC’ và BD’. 

Theo kết quả của Ví dụ 3, các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.

=> đi qua O.
Vậy bốn mặt phẳng cùng đi qua một điểm.

BT 1 trang 113 sgk toán 11 cánh diều

Cho hình hộp ABCD.A'B'C'D'.

a) Chứng minh rằng (ACB') ∥ (A'C'D). 

b) Gọi G₁,G₂ lần lượt là giao điểm của BD' với các mặt phẳng (ACB') và (A'C'D). Chứng minh rằng G₁,G₂ lần lượt là trọng tâm của hai tam giác ACB' và A'C'D. 

c) Chứng minh rằng BG₁ = G₁G₂ = D’G₂. 

Trả lời rút gọn:

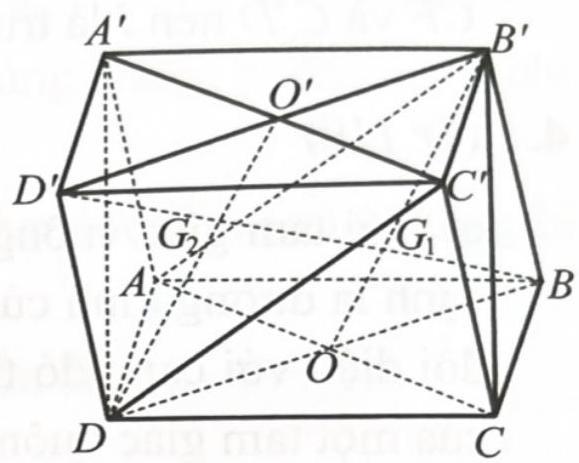
a) Tứ giác có và (tính chất hình hộp) nên tứ giác là hình bình hành. 

=> , mà =>.

Tương tự, tứ giác cũng là hình bình hành nên , mà  

=> 

Từ (1) và => .

b) Gọi và lần lượt là tâm của các hình bình hành và .

Gọi lần lượt là giao điểm của ' với và .

và .

Mà =>.

 Xét tam giác có trung tuyến và .

=> là trọng tâm của tam giác .

Chứng minh tương tự, ta cũng có là trọng tâm của tam giác .

c) Trong mặt phẳng có nên hay . 

Tương tự, ta cũng có

=> .

BT 2 trang 113 sgk toán 11 cánh diều

Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA', C'D', AD'. Chứng minh rằng: 

a) NQ ∥ A'D' và NQ = ½.A'D';

b) Tứ giác MNQC là hình bình hành

c) MN ∥ (ACD')

d) (MNP) ∥ (ACD'). 

Trả lời rút gọn:

a)

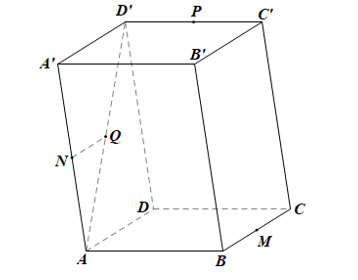
+) Xét có N, Q lần lượt là trung điểm của AA’ và AD’

Do đó NQ là đường trung bình của tam giác

=> và

b)

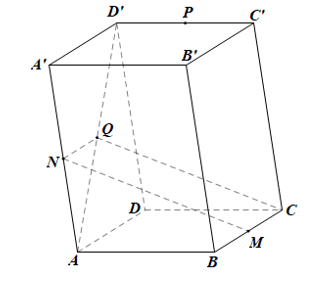
nên NQ // BC hay NQ // MC.

mà  nên

=>NQ = MC.

Tứ giác MNQC có và NQ = MC nên là MNQC hình bình hành.

c)

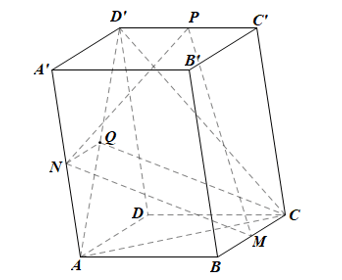
Do MNQC hình bình hành nên MN // QC

Mà nên

d)

Gọi O là trung điểm của ABCD.

+) Xét tam giác ABC có O, M lần lượt là trung điểm của AC, BC nên OM là đường trung bình của tam giác

=> OM // AB và

và D’C’ = AB nên OM = D’P.

+) Xét tứ giác D’PMO có OM // D’P và OM = D’P nên D’PMO là hình bình hành

=> PM // D’O

Mà ) nên

+)

           MN, PM cắt nhau tại điểm M và cùng nằm trong mp(MNP)

=>

BT 3 trang 113 sgk toán 11 cánh diều

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi E, F lần lượt là trung điểm của các cạnh AC và A'B'.

a) Chứng minh rằng EF ∥ (BCC'B'). 

b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC'B). Chứng minh rằng I là trung điểm của đoạn thẳng CF.

Trả lời rút gọn:

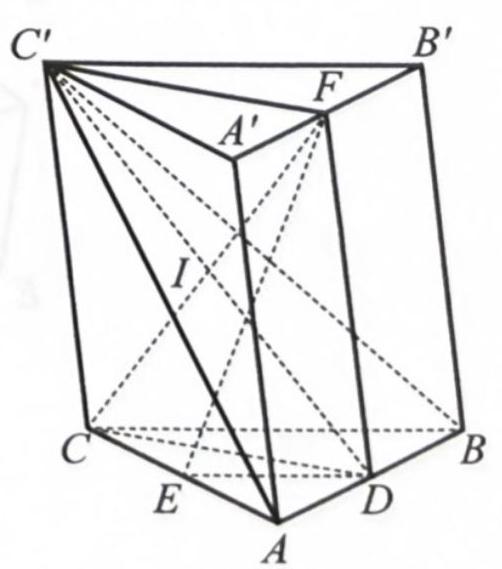
a) Lấy là trung điểm của (Hinh 15. 

Tứ giác là hình bình hành nên

  =>.

Do là đường trung bình tam giác nên

=>.

Từ (1) và (2) => .

=>

Trong mặt phẳng , gọi là giao điểm của và

 Do nên thuộc mặt phẳng

=> là giao điểm của đường thẳng với mặt phẳng .

Tứ giác có (vì cùng song song với ) và (cùng bằng ).

Do đó, tứ giác là hình bình hành nên là giao điểm của hai đường chéo và nên là trung điểm của .