Slide bài giảng Toán 11 cánh diều Chương 4 Bài 4: Hai mặt phẳng song song

Tóm lược nội dung

BÀI 4. HAI MẶT PHẲNG SONG SONG

I. HAI MẶT PHẲNG SONG SONG

LT-VD 1 trang 105 sgk toán 11 cánh diều

Nêu ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng song song.

Trả lời rút gọn:

Hình ảnh hai mặt phẳng song song: Các mặt sàn của ngôi nhà nhiều tầng; các mặt bậc cầu thang; mặt bàn và nền nhà; …

II. ĐIỀU KIỆN VÀ TÍNH CHẤT

LT-VD 2 trang 106 sgk toán 11 cánh diều 

Cho tứ diện ABCD. Các điểm M, N, P, I, J, K lần lượt là trung điểm của BC, CD, DB, AM, AN, AP. Chứng minh rằng (IJK) ∥ (BCD). 

Trả lời rút gọn:

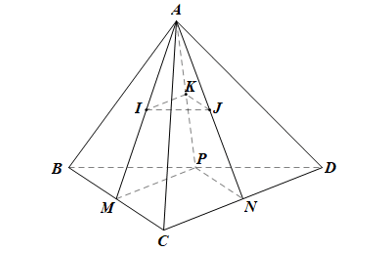
+) Xét có I, K lần lượt là trung điểm của AM, AP nên IK là đường trung bình

=>

Mà ) nên

+) Xét có J, K lần lượt là trung điểm của AN, AP nên JK là đường trung bình

=>

Mà ) nên

+)

=>

LT-VD 3 trang 108 sgk toán 11 cánh diều

Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A', B'. Chứng minh rằng AB = A'B'. 

Trả lời rút gọn:

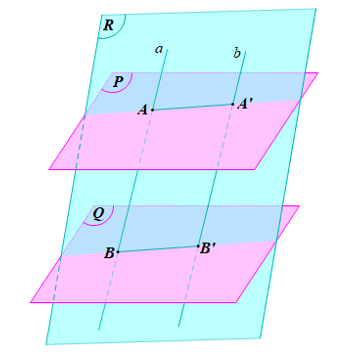
Giả sử

và  

=>

Tương tự ta cũng có

Do

=>

Trong mp(R), xét tứ giác ABB’A’ có:

=> ABB’A’ là hình bình hành

=>

III. ĐỊNH LÍ THALÈS

LT-VD 4 trang 109 sgk toán 11 cánh diều

Bạn Minh cho rằng: Nếu a, b là hai cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A', B', C' thì... Phát biểu của bạn Minh có đúng không? Vì sao?

Trả lời rút gọn:

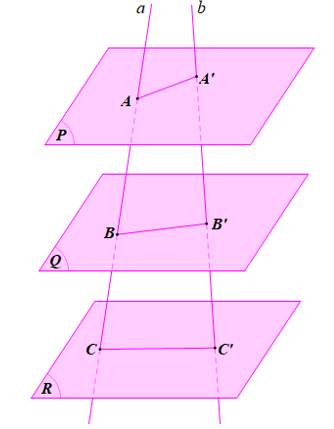
Theo định lí Thalès, nếu là hai cát tuyến bất kì cắt ba mặt phẳng song song lần lượt tại các điểm và thì .
Bạn Minh phát biểu rằng
Mà  nên phát biểu của bạn Minh là sai.

BT 1 trang 109 sgk toán 11 cánh diều

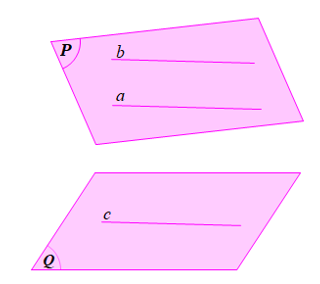
Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao? 

Trả lời rút gọn:

Phát biểu của bạn Chung không đúng, để (P) // (Q) thì hai đường thẳng a và b trong mặt phẳng (P) cần thêm điều kiện cắt nhau tại một điểm.

Ví dụ: nhưng (P) cắt (Q) (hình vẽ)

BT 2 trang 109 sgk toán 11 cánh diều

Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trong mặt phẳng (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A', B', C', D'. Chứng minh rằng A'B'C'D' là hình bình hành.

Trả lời rút gọn:

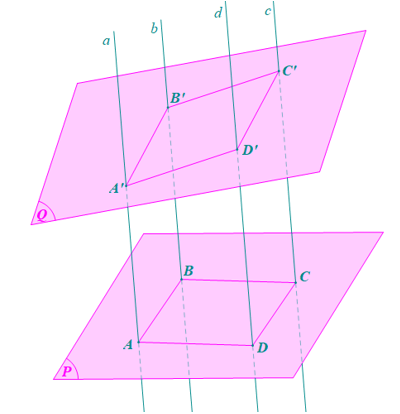
+) (do là hình bình hành).
Mà nên .
+)  a // d nên A'A // D'D
Mà nên .
+) ; ;
cắt nhau tại và cùng nằm trong

+)

=> .
Chứng minh tương tự: .
+) Tứ giác có và nên là hình bình hành.

BT 3 trang 109 sgk toán 11 cánh diều

Cho tứ diện ABCD. Lấy G₁,G₂,G₃ lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. 

a) Chứng minh rằng (G₁G₂G₃)∥(BCD).

b) Xác định giao tuyến của mặt phẳng (G₁G₂G₃) với mặt phẳng (ABD). 

Trả lời rút gọn:

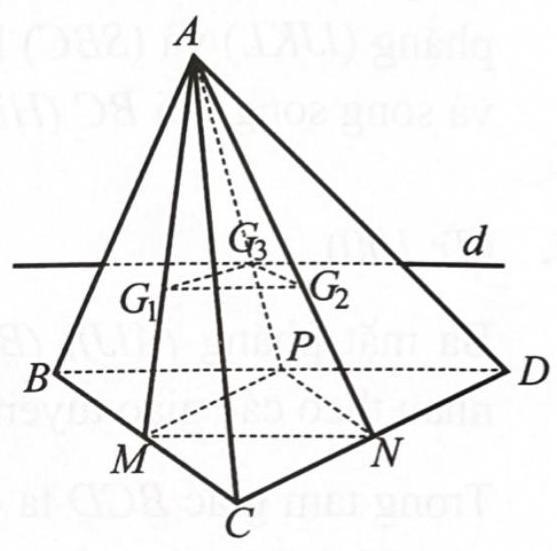
a) Gọi lần lượt là trung điểm của , .

và và .

=>

=> .

Mà nên .

Chứng minh tương tự . 

Mà => (2).

 Từ (1) và (2) => .

b) Do là một điểm chung của hai mặt phẳng và  

=> Theo định lý 3 tại một đường thẳng đi qua và song song với .

BT 4 trang 109 sgk toán 11 cánh diều

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. 

a) Chứng minh rằng (AFD) ∥ (BEC). 

b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính AN/NC. 

Trả lời rút gọn:

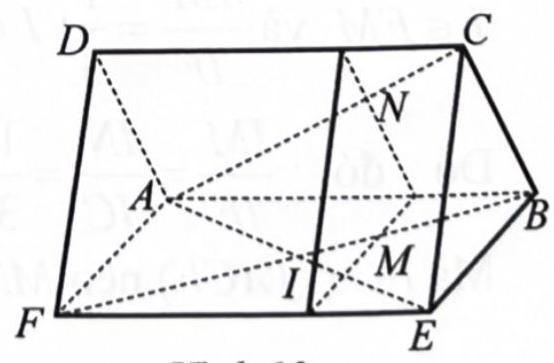
a) Vì là hình bình hành nên . 

Mà không thuộc mặt phẳng =>. 

Tương tự, do là hình bình hành nên => . 

Mà , cắt nhau và nằm trong mặt phẳng nên theo Định lí 1 .

b) Gọi là giao điểm của và

là trung điểm mà là trọng tâm của tam giác nên và , hay . 

cắt ba mặt phẳng song song lần lượt tại . Đường thẳng cũng cắt ba mặt phẳng trên theo thứ tự . 

Áp dụng định lí Thalès trong không gian . 

Vậy