Slide bài giảng Toán 11 cánh diều Bài tập cuối chương 5

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG V

Bài 1: Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm 100. Kết quả được trình bày trong Bảng 16…

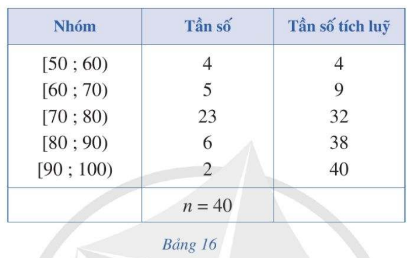
Trả lời rút gọn:

a) B

b)  D

c)  C

Bài 2: Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:…

Trả lời rút gọn:

C

Để hai số có tổng là một số chẵn là thì có các trường hợp sau:

TH1: Cả hai số là số chẵn; TH2: Cả hai số là số lẻ

“Cả hai số là số chẵn”

=>

: “Cả hai số là số lẻ”

=>

Vậy xác suất để chọn được hai số có tổng là một số chẵn là:

Bài 3: Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của 40 chiếc ô tô:…

Trả lời rút gọn:

a) Bảng tần số ghép nhóm cho mẫu số liệu trên có năm nhóm ứng với năm nửa khoảng:

b) 

-   

-

-

-

- 

c)

Bài 4: Bạn Dũng và bạn Hương tham gia đội văn nghệ của nhà trường. Nhà trường chọn từ đội văn nghệ đó một bạn nam và một bạn nữ để lập tiết mục song ca. Xác suất được nhà trường chọn vào tiết mục song ca của Dũng và Hương lần lượt là 0,7 và 0,9.

Trả lời rút gọn:

a)

b) : "Dũng không được chọn"

: "Hương không được chọn"

=>

c)

Bài 5: Hai bạn Mai và Thi cùng tham gia một kỳ kiểm tra ngoại ngữ một cách độc lập nhau. Xác suất để bạn Mai và bạn Thi đạt từ điểm 7 trở lên lần lượt là 0,8 và 0,9. Tính xác suất của biến cố C: “Cả hai bạn đều đạt từ điểm 7 trở lên”.

Trả lời rút gọn:

“Bạn Mai thi được từ 7 điểm trở lên”

: “Bạn Thi thi được từ 7 điểm trở lên”

  =>

Bài 6: Một người chọn ngẫu nhiên 3 lá thư vào 3 phong bì đã ghi địa chỉ sao cho mỗi phong bì chỉ chứa một lá thư. Tính xác suất để có ít nhất một lá thư được cho vào đúng phong bì đã ghi địa chỉ theo lá thư đó.

Trả lời rút gọn:

-

- Gọi : “Không lá thư nào được bỏ đúng phong bì”

: “Có ít nhất một lá thư được bỏ đúng phong bì”

=> =>

=>

Bài 7: Một hộp chứa 9 quả cầu có cùng kích thước và khối lượng. Trong đó có 4 quả cầu màu xanh đánh số từ 1 đến 4, có 3 quả cầu màu vàng đánh số từ 1 đến 3, có 2 quả cầu màu đỏ đánh số từ 1 đến 2. Lấy ngẫu nhiên 2 quả cầu từ hộp. Tính xác suất để 2 quả cầu được lấy vừa khác màu vừa khác số.

Trả lời rút gọn:

-

- Số cách lấy 2 quả khác màu là:

+ 1 quả màu xanh và 1 quả màu vàng:

+ 1 quả màu xanh và 1 quả màu đỏ:

+ 1 quả màu đỏ và 1 quả màu vàng:

=> Tổng số cách lấy ra 2 quả khác màu là : cách

- Số cách lấy 2 quả khác nhau trùng số:

+ 2 quả cùng là số 1:

+ 2 quả cùng là số 2:

+ 2 quả cùng là số 3:

=> Tổng số cách lấy ra 2 quả khác màu trùng số là: 7 cách

=> Số cách lấy ra 2 quả khác màu khác số là: (cách)

=> Xác suất để lấy ra 2 quả khác màu khác số là:

Bài 8: Để nghiên cứu xác suất của một loại cây trồng mới phát triển bình thường, người ta trồng hạt giống của loại cây đó trên hai lô đất thí nghiệm A, B khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các lô đất A, B lần lượt là 0,7 và 0,6. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng, tính xác suất hạt giống chỉ phát triển bình thường trên một lô đất.

Trả lời rút gọn:

là xác suất hạt giống phát triển bình thường trên lô đất

là xác suất hạt giống phát triển bình thường trên lô đất

là xác suất hạt giống không phát triển bình thường trên lô đất

là xác suất hạt giống không phát triển bình thường trên lô đất

=>

=>

Vậy, xác suất hạt giống phát triển bình thường trên một lô đất là: