Slide bài giảng Toán 11 cánh diều Chương 2 Bài 3: Cấp số nhân

Tóm lược nội dung

BÀI 3: CẤP SỐ NHÂN

I. ĐỊNH NGHĨA

LT-VD 1 trang 53 sgk toán 11 cánh diều

Cho cấp số nhân (u_n) với u₁ = −6, u₂ = −2. 

a) Tìm công bội q

b) Viết năm số hạng đầu của cấp số nhân đó

Trả lời rút gọn:

a) 

b) 

.

LT-VD 2 trang 54 sgk toán 11 cánh diều

Cho dãy số (un) với u_n = 3.2ⁿ ( n≥1 ). Dãy (u_n) có là cấp số nhân không? Vì sao?

Trả lời rút gọn:

=> với

Vì vậy dãy là cấp số nhân có số hạng đầu và công bội .

II. SỐ HẠNG TỔNG QUÁT

LT-VD 3 trang 55 sgk toán 11 cánh diều

Bác Linh gửi vào ngân hàng 100 triệu đồng tiền tiết kiệm với hình thức lãi kép, kì hạn 1 năm với lãi suất 6%/năm. Viết công thức tính số tiền (cả gốc và lãi) mà bác Linh có được sau n năm (giả sử lãi suất không thay đổi qua các năm)

Trả lời rút gọn:

Số tiền ban đầu T₁ = 100 (triệu đồng).

Số tiền sau 1 năm bác Linh thu được là:

(Triệu đồng).

Số tiền sau 2 năm bác Linh thu được là:

(Triệu đồng)

Số tiền sau 3 năm bác Linh thu được là:

(Triệu đồng). 

Số tiền sau n năm bác Linh thu được chính là một cấp số nhân với số hạng đầu và công bội có số hạng tổng quát là:

(Triệu đồng)

III. TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ NHÂN

LT-VD 4 trang 55 sgk toán 11 cánh diều

Tính tổng n số hạng đầu của mỗi cấp số nhân sau:

a) 3,−6,12,−24,... với n = 12

b) 1/10, 1/100, 1/1000 với n = 5

Trả lời rút gọn:

a) 3; – 6; 12; – 24; ... là cấp số nhân với và công bội

b) là một cấp số nhân với và công bội .

BT 1 trang 56 sgk toán 11 cánh diều

Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a) 5; −0,5; 0,05; −0,005; 0,0005

b) −9, 3, −1, 1/3, −1/9

c) 2, 8, 32, 64, 256

Trả lời rút gọn:

a)

dãy trên là cấp số nhân với số hạng đầu và công bội

b) 

dãy trên là cấp số nhân với số hạng đầu và công bội .

c)

Vì vậy dãy trên không là cấp số nhân.

BT 2 trang 56 sgk toán 11 cánh diều

Chứng minh mỗi dãy số (u_n) với số hạng tổng quát như sau là cấp số nhân...

Trả lời rút gọn:

a) 

Vì vậy dãy số đã cho là một cấp số nhân.

b) 

Vì vậy dãy số đã cho là một cấp số nhân.

c) 

Vì vậy dãy số đã cho là một cấp số nhân.

BT 3 trang 56 sgk toán 11 cánh diều

Cho cấp số nhân (u_n) với số hạng đầu u_n = −5, công bội q = 2. 

a) Tìm u₉. 

b) Số −320 là số hạng thứ bao nhiêu của cấp số nhân trên?

c) Số 160 có phải là một số hạng của cấp số nhân trên không?

Trả lời rút gọn:

a)  là cấp số nhân có số hạng đầu và công bội với mọi .

=>

b) 

Vậy số – 320 là số hạng thứ 7 của cấp số nhân.

c) 

Vậy số 160 không phải là một số hạng của cấp số nhân.

BT 4 trang 56 sgk toán 11 cánh diều

Cho cấp số nhân (u_n) với u₁ = 3, u₃ = 27/4

a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên

b) Tính tổng 10 số hạng đầu của cấp số nhân trên

Trả lời rút gọn:

a) 

Xét

+ Với ta có 

;

.

+ Với ta có 

b)

+)  

+) : 

BT 5 trang 56 sgk toán 11 cánh diều

Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi u_n là dân số của tỉnh đó sau n năm. Giả sử tỉ lệ tăng dân số là không đổi

a) Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020

b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020

Trả lời rút gọn:

a)  lập thành một cấp số nhân có số hạng đầu là triệu dân và công sai

(triệu dân).

b) Số dân của tỉnh đó sau 10 năm kể từ năm 2020 là:

(triệu dân).

BT 6 trang 56 sgk toán 11 cánh diều

Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó). 

a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng. 

b) Viết công thức tính giá trị của ô tô sau n năm sử dụng. 

c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?

Trả lời rút gọn:

a) Sau 1 năm giá trị của ô tô còn lại là:

(triệu đồng)

Sau 2 năm giá trị của ô tô còn lại là:

(triệu đồng)

b) Gọi là giá trị của ô tô sau n năm sử dụng.

Dãy số tạo thành một cấp số nhân với số hạng đầu là triệu đồng và công bội

=>

c) 

(triệu đồng).

BT 7 trang 56 sgk toán 11 cánh diều

Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100 m. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống. 

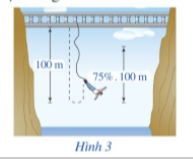
Trả lời rút gọn:

Gọi là quãng đường người chơi rơi xuống ở lần 1, 

Gọi là quãng đường người chơi được kéo lên ở lần 1,

+) là quãng đường người chơi rơi xuống ở lần 2, ta có

Gọi là quãng đường người chơi được kéo lên ở lần 2, ta có

+) Vậy ta có hai cấp số nhân đều có công bội 0,75 là: và ; với

Tổng quãng đường người đó đi được sau 10 lần rơi xuống và được kéo lên tính từ lúc bắt đầu nhảy là :