Slide bài giảng Toán 11 cánh diều Chương 1 Bài 3: Hàm số lượng giác và đồ thị
Slide điện tử Chương 1 Bài 3: Hàm số lượng giác và đồ thị. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3: HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
I. HÀM SỐ CHẴN, HÀM SỐ LẺ, HÀM SỐ TUẦN HOÀN
LT-VD 1 trang 23 sgk toán 11 cánh diều
a) Chứng tỏ rằng hàm số g(x)=... là hàm số lẻ.
b) Cho ví dụ về hàm số không là hàm số chẵn và cũng không là hàm số lẻ.
Trả lời rút gọn:
a) ![]() có
có ![]() .
.
![]() thì
thì ![]()
![]()
=> ![]() là hàm số lẻ.
là hàm số lẻ.
b) hàm số không là hàm số chẵn và cũng không là hàm số lẻ:
![]()
LT-VD 2 trang 23 sgk toán 11 cánh diều
Cho ví dụ về hàm số tuần hoàn.
Trả lời rút gọn:
Ví dụ về hàm số tuần hoàn:
Cho T là một số hữu tỉ và hàm số f(x) được cho bởi công thức sau:
![]()
![]() có D=
có D=![]() .
.
Nếu x là số hữu tỉ thì x + T cũng là số hữu tỉ;
Nếu x là số vô tỉ thì x + T cũng là số vô tỉ.
=> f(x + T) = f(x) với mọi x.
Vậy hàm số f(x) là hàm số tuần hoàn.
II. HÀM SỐ Y = SINX
LT-VD 3 trang 25 sgk toán 11 cánh diều
Hàm số y = sinx đồng biến hay nghịch biến trên khoảng...
Trả lời rút gọn:
![]()
![]() nên hàm số
nên hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
III. HÀM SỐ Y = COSX
LT-VD 4 trang 27 sgk toán 11 cánh diều
Hàm số y = cosx đồng biến hay nghịch biến trên khoảng (−2π;−π)
Trả lời rút gọn:
![]()
=> hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
IV. HÀM SỐ Y = TANX
LT-VD 5 trang 29 sgk toán 11 cánh diều
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = tanx trên khoảng...
Trả lời rút gọn:
Xét đồ thị của hàm số y = m và đồ thị của hàm số y = tan x trên khoảng ![]()
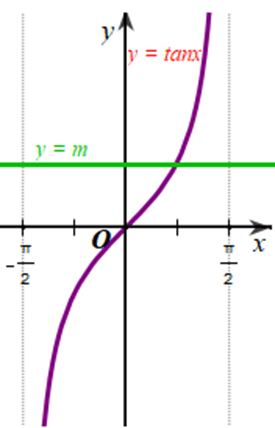
Từ đồ thị của hai hàm số trên hình vẽ => số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = tan x trên khoảng ![]() là 1.
là 1.
V. HÀM SỐ Y = COTX
LT-VD 6 trang 30 sgk toán 11 cánh diều
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = cotx trên khoảng (0,π).
Trả lời rút gọn:
Xét đồ thị của hàm số y = m và đồ thị của hàm số y = cot x trên khoảng (0; π) (hình vẽ).
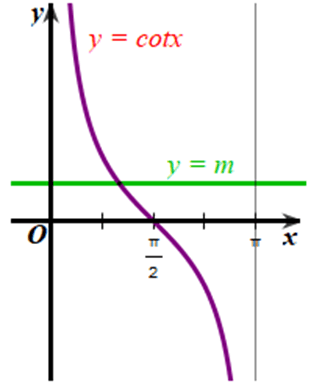
Từ đồ thị của hai hàm số trên hình vẽ =>số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = cot x trên khoảng (0; π) là 1.
BT 1 trang 31 sgk toán 11 cánh diều
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [−2π;2π] để:
a) Hàm số y = sinx nhận giá trị bằng 1
b) Hàm số y = sinx nhận giá trị bằng 0
c) Hàm số y = cosx nhận giá trị bằng -1
d) Hàm số y = cosx nhận giá trị bằng 0
Trả lời rút gọn:
* Đồ thị hàm số y = sinx:
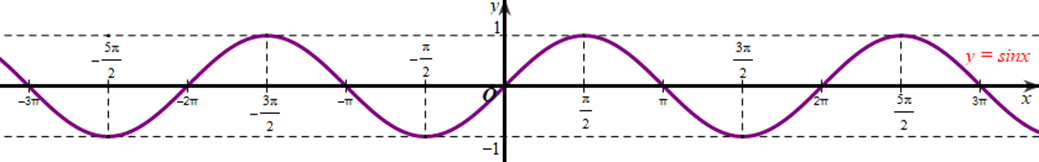
a) ta thấy hàm số ![]() nhận giá trị bằng 1 tại
nhận giá trị bằng 1 tại ![]() .
.
b) Ta thấy hàm số ![]() nhận giá trị bằng 0 tại
nhận giá trị bằng 0 tại ![]()
* Đồ thị hàm số y = cosx:

c) Ta thấy hàm số ![]() nhận giá trị bằng 1 tại
nhận giá trị bằng 1 tại ![]() .
.
d) Ta thấy hàm số ![]() nhận giá trị bằng 0 tại
nhận giá trị bằng 0 tại ![]() .
.
BT 2 trang 31 sgk toán 11 cánh diều
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (−π; 3π/2) để:
a) Hàm số y = tanx nhận giá trị bằng -1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
Trả lời rút gọn:
a) Xét đồ thị hàm số ![]() và đồ thị hàm số
và đồ thị hàm số ![]() trên khoảng
trên khoảng ![]() :
:
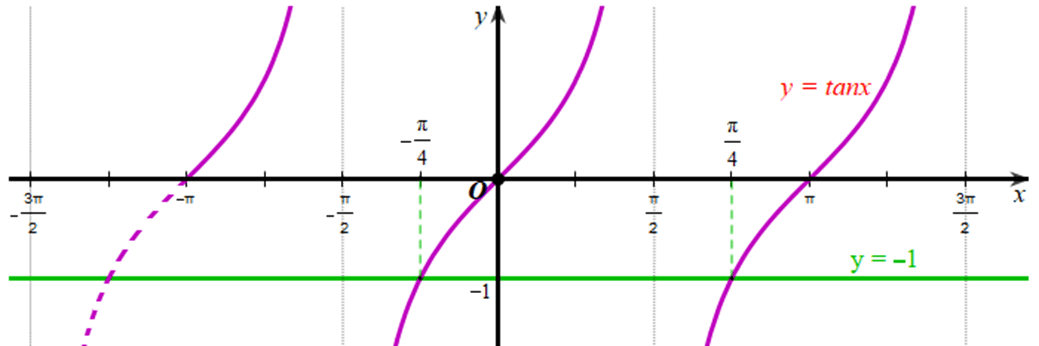
![]() nhận giá trị bằng ‒1 tại
nhận giá trị bằng ‒1 tại ![]() .
.
b) Xét đồ thị hàm số ![]() trên khoảng
trên khoảng ![]() :
:
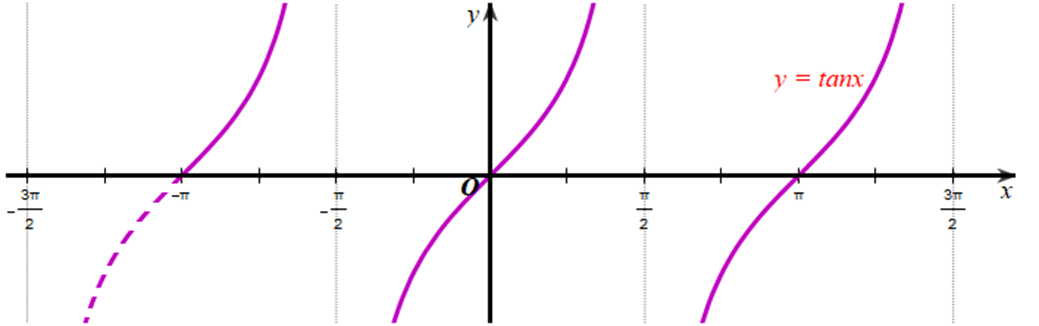
ta thấy hàm số ![]() nhận giá trị bằng 0 tại
nhận giá trị bằng 0 tại ![]() .
.
c) Xét đồ thị hàm số ![]() và đồ thị hàm số
và đồ thị hàm số ![]() trên khoảng
trên khoảng ![]() :
:
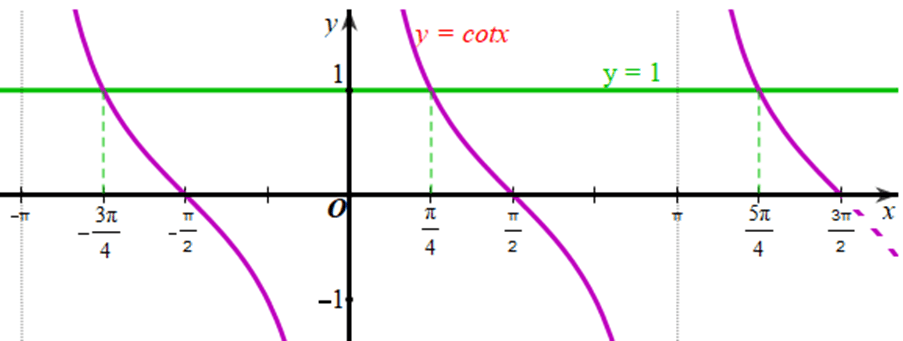
ta thấy hàm số ![]() nhận giá trị bằng 1 tại
nhận giá trị bằng 1 tại ![]()
d) Xét đồ thị hàm số ![]() trên khoảng
trên khoảng ![]() :
:

ta thấy hàm số ![]() nhận giá trị bằng 0 tại
nhận giá trị bằng 0 tại ![]() .
.
