CHƯƠNG 1: SỐ TỰ NHIÊN

BÀI 12: ƯỚC CHUNG VÀ ƯỚC CHUNG LỚN NHẤT

1. ƯỚC CHUNG VÀ ƯỚC CHUNG LỚN NHẤT

Bài 1: a) Nêu các ước của 30 và của 48 theo thứ tự tăng dần:

b) Tìm các số vừa ở trong hàng thứ nhất vừa ở trong hàng thứ hai.

c) Xác định số lớn nhất trong các ước chung của 30 và 48.

Giải nhanh:

a)

b) 30 và 48

c) 6

Bài 2: a) Số 8 có phải là ước chung của 24 và 56 không? Vì sao?

b) Số 8 có phải là ước chung của 14 và 48 không? Vì sao?

Giải nhanh:

a) 8 là ước chung của 24 và 56. 

b) 8 không phải là ước chung của 14 và 48. 

Bài 3: Số 7 có phải là ước chung của 14, 49, 63 không? Vì sao?

Giải nhanh:

7 là ước chung của ba số 14; 49 và 63. 

Bài 4: Quan sát bảng sau:

a) Viết tập hợp ƯC(24, 36).

b) Tìm ƯCLN (24, 36).

c) Thực hiện phép chia ƯCLN (24, 36) cho các ước chung của hai số đó.

Giải nhanh:

a) ƯC(24, 36) = {1; 2; 3; 4; 6; 12}. 

b) ƯCLN(24, 36) = 12. 

c)  

12 : 1 = 12

12 : 2 = 6 

12 : 3 = 4

12 : 4 = 3 

12 : 6 = 2 

12 : 12 = 1.

Bài 5: Tìm tất cả các số có hai chữ số là ước chung của a và b, biết rằng ƯCLN(a, b) = 80.

Giải nhanh:

ƯC (a, b) = {10; 16; 20; 40; 80}  

1. TÌM ƯỚC CHUNG LỚN NHẤT BẰNG CÁCH PHÂN TÍCH CÁC SỐ RA THỪA SỐ NGUYÊN TỐ

Bài 1: Ta có thể tìm ƯCLN (36, 48)

Giải nhanh:

Bước 1. Phân tích 36 và 48 ra thừa số nguyên tố

          36 = 2² . 3²

          48 = 2⁴ . 3

Bước 2. Chọn ra các thừa số nguyên tố chung của 36 và 48 là 2 và 3.

Bước 3. Với mỗi thừa số nguyên tố chung 2 và 3, ta chọn lũy thừa với số mũ nhỏ nhất

+) Số mũ nhỏ nhất của 2 là 2, ta chọn 2².

+) Số mũ nhỏ nhất của 3 là 1, ta chọn 3¹.

Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm ƯCLN (36, 48) = 12

Bài 2: Tìm ƯCLN của 126, 162

Giải nhanh: 

126 = 2. 3 . 3. 7= 2 . 3² . 7 

162 = 2 . 3. 3. 3. 3 = 2 . 3⁴

ƯCLN(126, 162) = 2¹ . 3² = 18.

3. HAI SỐ NGUYÊN TỐ CÙNG NHAU

Bài 1: Tìm ƯCLN(8, 27).

Giải nhanh: 

24 = 2³ . 3 và 35 = 5 . 7 

ƯCLN(24, 35) = 1 

Vậy 24 và 35 là hai số nguyên tố cùng nhau

Bài 2: Hai số 24 và 35 có nguyên tố cùng nhau không? Vì sao?

Giải nhanh: 

24 = 2³ . 3 và 35 = 5 . 7 

ƯCLN(24, 35) = 1. 

Vậy 24 và 35 là hai số nguyên tố cùng nhau.

Bài 3: a) Tìm ƯCLN(4, 9).

b) Có thể rút gọn phân số được nữa hay không?

Giải nhanh: 

a) Ta có: 4 = 2 . 2 = 2² và 9 = 3 . 3 = 3² 

Do đó hai số 4 và 9 không có thừa số nguyên tố chung nên ƯCLN(4, 9) = 1. 

b) Không thể 

BÀI TẬP

Bài 1: Số 1 có phải là ước chung của hai số tự nhiên bất kì không? Vì sao?

Giải nhanh: 

Đúng vì tất cả các số tự nhiên đều có ước là 1

Bài 2: Quan sát hai thanh sau:

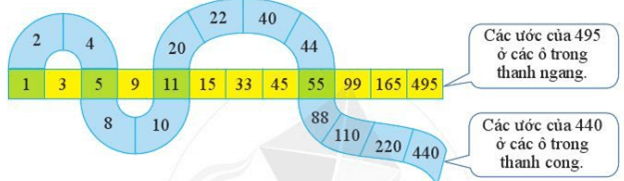
a) Viết tập hợp ƯC(440, 495).

b) Tìm ƯCLN(440, 495). 

Giải nhanh: 

a) 

+ Ư (440) = {1; 2; 4; 5; 8; 10; 11; 20; 22; 40; 44; 55; 88; 110; 220; 440}

+ Ư (495) = {1; 3; 5; 9; 11; 15; 33; 45; 55; 99; 165; 495}

=> ƯC(440, 495) = {1; 5; 11; 55}

b) ƯCLN(440, 495) = 55.

Bài 3: Tìm ước chung lớn nhất của từng cặp số trong ba số sau đây:

a) 31, 22, 34;

b) 105, 128, 135; 

Giải nhanh: 

a) ƯCLN(31, 22) = 1; ƯCLN(31, 34) = 1; ƯCLN( 22, 34) = 2. 

b)ƯCLN(105, 128) = 1; ƯCLN(128, 135) = 1 và ƯCLN(105, 135) = 15

Bài 4: Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126 và 150.

Giải nhanh: 

126 = 2 . 3 . 3 . 7 = 2 . 3² . 7

150 = 2 . 3 . 5 . 5 = 2 . 3 . 5²

=> ƯCLN(126, 150) = 2¹ . 3¹ = 2 . 3 = 6 

=> ƯC(126, 150) = {1; 2; 3; 6} 

Bài 5: Rút gọn các phân số sau về phân số tối giản

Giải nhanh: 

= 

= 

= 

Bài 6: Phân số  bằng các phân số nào trong các phân số sau

Giải nhanh: 

.

.

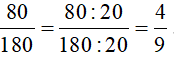
Vậy trong các phân số đã cho, các phân số bằng là 

Bài 7: Một nhóm gồm 24 bạn nữ và 30 bạn nam tham gia một số trò chơi. Có thể chia các bạn thành nhiều nhất bao nhiêu đội chơi sao cho số bạn nam cũng như số bạn nữ được chia đều vào các đội?

Giải nhanh: 

Giả sử a là số đội chơi được chia. (a ∈ )

 Vì a là lớn nhất (phải chia nhiều đội nhất) và số bạn nam cũng như số bạn nữ được chia đều vào các đội nên khi đó a là ƯCLN (24, 30) 

Ta có: 24 = 3 . 8 = 3 . 2³ ; 30 = 3 . 10 = 3 . 2 . 5 

Khi đó: ƯCLN(24, 30) = 2 . 3 = 6 hay a = 6. 

Vậy có thể chia các bạn nhiều nhất thành 6 đội. 

Bài 8: Một khu đất có dạng hình chữ nhật với chiều dài 48m, chiều rộng 42m. Người ta muốn chia khu đất ấy thành những mảnh hình vuông bằng nhau (với độ dài cạnh đo theo đơn vị mét là số tự nhiên) để trồng các loại rau. Có thể chia được bằng bao nhiêu cách? Với cách chia nào thì cạnh của mảnh đất hình vuông là lớn nhất và bằng bao nhiêu?

Giải nhanh: 

Gọi a là số cách chia mảnh đất thành các mảnh hình vuông bằng nhau và b (m) là độ dài cạnh của mảnh đất hình vuông được chia theo cách chia lớn nhất a,b ∈

=> a là ƯC (48, 42)

=> b là ƯCLN (48, 42)

Ta có: 

• 42 = 2 . 21 = 2 . 3 . 7 
• 48 = 16 . 3 = 2⁴ . 3

=> ƯCLN(42, 48) = 2 . 3 = 6 hay b = 6 m 

Mà Ư(6) = {1; 2; 3; 6) Nên ƯC(42, 48) = {1; 2; 3; 6}

Do đó có 4 ước chung của 42 và 48 hay a = 4.

Vậy:

+ Số cách chia thành những mảnh hình vuông bằng nhau là 4 cách.

+ Với cách chia có độ dài cạnh là 6m thì cạnh của mảnh đất hình vuông là lớn nhất. 

CÓ THỂ EM CHƯA BIẾT

Áp dụng thuật toán Ơ-clit để tìm ƯCLN của:

a) 126 và 162;

b) 2 268 và 1 260.

Giải nhanh: 

a)

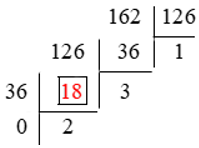
Bước 1: 162 : 126 = 1 (dư 36) (1)

Bước 2: 

+) Phép chia (1) còn dư nên lấy số chia 126 chia cho số dư 36

126 : 36 = 3 (dư 18) (2)

+) Phép chia (2) còn dư nên lấy số chia 36 chia cho số dư 18

36 : 18 = 2 (dư 0) (3)

Phép chia (3) có số dư bằng 0, ta dừng lại.

Bước 3: ƯCLN(162, 126) = 18.

b) 

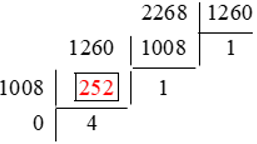
Bước 1: 2 268 : 1 260 = 1 (dư 1 008) (1)

Bước 2: 

+) Phép chia (1) còn dư nên lấy số chia 1 260 chia cho số dư 1 008

1 260 : 1 008 = 1 (dư 252) (2)

+) Phép chia (2) còn dư nên lấy số chia 1 008 chia cho số dư 252

1 008 : 252 = 4 (dư 0) (3)

Phép chia (3) có số dư bằng 0, ta dừng lại.

Bước 3: ƯCLN(2 268, 1 260) = 252