CHƯƠNG II: SỐ NGUYÊN

BÀI 6: PHÉP CHIA HẾT HAI SỐ NGUYÊN. QUAN HỆ CHIA HẾT TRONG TẬP HỢP SỐ NGUYÊN

1. PHÉP CHIA HAI SỐ NGUYÊN KHÁC DẤU

Bài 1: a) Tìm số thích hợp cho (?) : Do (– 3) . (– 4) = 12 nên 12 : (– 3) = (?)

Mẫu: Do 4 . (– 3) = – 12 nên (– 12) : 4 = – 3.

b) So sánh 12 : (– 3) và – (12 : 3).

Giải nhanh:

a) (?) là – 4.

b) 12 : (– 3) = – (12 : 3).

Bài 2: Tính:

a) 36 : (– 9);

b) (– 48) : 6.

Giải nhanh:

a) – 4

b) – 8 

2. PHÉP CHIA HẾT HAI SỐ NGUYÊN CÙNG DẤU

Bài 1: a) Tìm số thích hợp cho (?) : Do (– 5) . 4 = – 20 nên (– 20) : (– 5) = (?)

Mẫu: Do (– 4) . 3 = – 12 nên (– 12) : (– 4) = 3.

b) So sánh (– 20) : (– 5) và 20 : 5.

Giải nhanh: 

a) (?) là 4. 

b) (– 20) : (– 5) = 20 : 5. 

Bài 2: Tính:

a) (– 12) : (– 6);

b) (– 64) : (– 8).

Giải nhanh: 

a) 2 

b) 8

3. QUAN HỆ CHIA HẾT

Bài 1: a) Tìm số thích hợp ở (?) trong bảng sau:

b) Số – 36 có thể chia hết cho các số nguyên nào?

Giải nhanh: 

a)

b) 1; 2; 3; 4; 6; 9; 12; 18; 36; – 1; – 2; – 3; – 4; – 6; – 9; – 12; – 18; – 36

Bài 2: Sử dụng các từ “chia hết cho”, "bội", “ước” thích hợp (?):

a) – 16 (?) – 2;

b) – 18 là (?) của – 6;

c) 3 là (?) của – 27.

Giải nhanh: 

a) "chia hết cho"

b) "bội"

c) "ước" 

Bài 3: a) Viết tất cả các số nguyên là ước của: – 15; – 12.

b) Viết năm số nguyên là bội của: – 3; – 7. 

Giải nhanh: 

a)  Ư (– 15) ={ – 1; 1; – 3; 3; –5; 5; –15; 15}

Ư (– 12) = {– 1; 1; – 2; 2; – 3; 3; – 4; 4; – 6; 6; – 12; 12}

b) B(– 3) ={– 3; 3; – 6; 6; – 9}

B (– 7) = {0; – 7; 7; – 14; 14}

BÀI TẬP

Bài 1: Tính:

a) (– 45) : 5; 

b) 56 : (– 7); 

c) 75 : 25; 

d) (– 207) : (– 9).

Giải nhanh: 

a) – 9 

b) – 8

c) 3

d) 23

Bài 2: So sánh:

a) 36 : (– 6) và 0; 

b) (– 15) : (– 3) và (– 63) : 7.

Giải nhanh: 

a) 36 : (– 6) < 0.

b) (– 15) : (– 3) > (– 63) : 7. 

Bài 3: Tìm số nguyên x, biết:

a) (– 3) . x = 36; 

b) (– 100) : (x + 5) = – 5.

Giải nhanh: 

a) x = – 12. 

b) x = 15. 

Bài 4: Nhiệt độ lúc 8 giờ sáng trong 5 ngày liên tiếp là – 6 °C, – 5 °C, – 4 °C, 2 °C, 3 °C. Tính nhiệt độ trung bình lúc 8 giờ sáng của 5 ngày đó.

Giải nhanh: 

– 2 °C

Bài 5: Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai? Giải thích.

a) – 36 chia hết cho – 9, 

b) – 18 chia hết cho 5.

Giải nhanh: 

a) Đúng. 

b) Ta có: – 18 = 5 . (– 3) + (– 3) 

Do đó – 18 không chia hết cho 5. 

Vậy phát biểu b) là sai

Bài 6: Tìm số nguyên x, biết:

a) 4 chia hết cho x; 

b) – 13 chia hết cho x + 2.

Giải nhanh: 

a)  – 1; 1; – 2; 2; – 4; 4.

b) Vì – 13 chia hết cho x + 2 nên x + 2 là Ư (– 13)

Mà Ư (– 13) = {– 1; 1; 13; – 13}

Nên ta có các trường hợp sau:

TH1: x + 2 = – 1  x = – 1 – 2 = – 3 (tm)

TH2: x + 2 = 1  x = 1 – 2 = – 1 (tm)

TH3: x + 2 = 13  x = 13 – 2 = 11 (tm)

TH4: x + 2 = – 13  x = – 13 – 2 = – 15 (tm)

Vậy các số nguyên x thỏa mãn yêu cầu bài toán là: – 3; – 1; 11; – 15.

Bài 7: Một con ốc sên leo lên một cây cao 8 m. Trong mỗi ngày (24 giờ), 12 giờ đầu tiên ốc sên leo lên được 3 m, rồi 12 giờ sau nó lại tụt xuống 2 m. Quy ước quãng đường mà ốc sên leo lên 3 m là 3 m, quãng đường ốc sên tụt xuống 2 m là – 2 m.

a) Viết phép tính biểu thị quãng đường mà ốc sên leo được sau 2 ngày.

b) Sau 5 ngày thi ốc sên leo được bao nhiêu mét?

c) Sau bao nhiêu giờ thi ốc sên chạm đến ngọn cây? Biết rằng lúc 0 giờ ốc sên ở gốc cây và bắt đầu leo lên.

Giải nhanh: 

a) Quãng đường mà ốc sên leo được trong 2 ngày được biểu thị bằng phép tính là: [3 + (– 2)] . 2         (m)

b) Sau 5 ngày, ốc sên leo được số m là: 

[3 + (– 2)] . 5 = 5 (m) 

c) Vì cây cao 8 m nên số giờ để ốc sên leo được 8 m chính là số giờ ốc sên chạm đến ngọn cây. 

Trong mỗi ngày, 12 giờ đầu tiên ốc sên leo được 3m, rồi 12 giờ sau nó lại tụt xuống 2m.

Vậy sau 1 ngày (24 giờ) ốc sên sẽ leo được 1 m

Đến hết ngày thứ 7 ốc sên leo được: 1 . 7 = 7 (m)

Sang ngày thứ 8, 12 giờ đầu ốc sên leo được 3 m, mà ốc sên chỉ cần leo thêm 1 m nữa là được 8 m . Thời gian để ốc sên leo được thêm 1 m nữa là: 12 : 3 = 4 (giờ)

Do đó trong 4 giờ đầu của ngày thứ 8, ốc sên leo được thêm 1 m nữa là được 8 m .

Nên tổng số giờ: 168 + 4 = 172 giờ.

Vậy sau 172 giờ leo cây thì ốc sên chạm đến ngọn cây. 

Bài 8: Sử dụng máy tính cầm tay

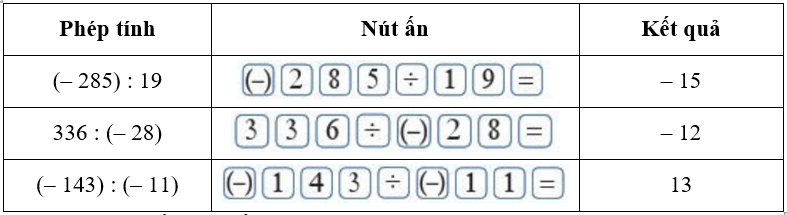
Dùng máy tính cầm tay để tính:

(– 252) : 21; 

253 : (– 11);

 (– 645) : (– 15).

Giải nhanh: 

(– 252) : 21 = – 12;

253 : (– 11) = – 23;

(– 645) : (– 15) = 43.